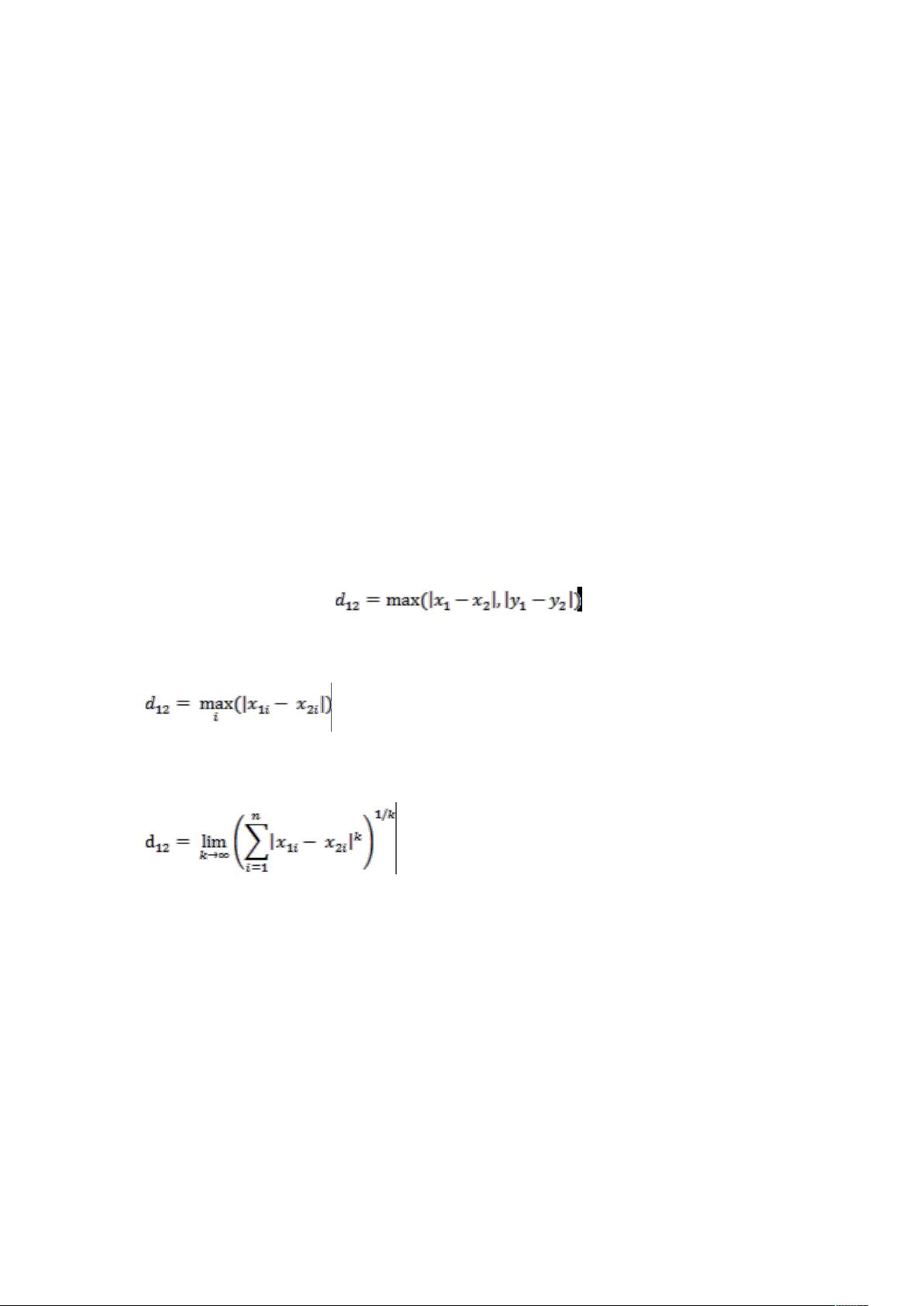机器学习：距离计算大全

"这篇文档汇总了机器学习中常用的多种距离计算方法，包括欧氏距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、标准化欧氏距离、马氏距离、夹角余弦、汉明距离、杰卡德距离和杰卡德相似系数、相关系数及相关距离以及信息熵。这些距离计算方法在评估样本间相似性时起着关键作用，对于分类任务尤其重要。文档详细介绍了每个距离的定义、计算公式以及在Matlab中的实现示例。" 1. 欧氏距离(EuclideanDistance)是最基本的距离度量，来源于几何学，适用于任意维度的空间。二维和三维空间中的欧氏距离公式分别给出了计算两点之间距离的方法。在n维空间中，欧氏距离通过计算两个向量各分量差的平方和再开方得到。在Matlab中，可以使用pdist函数计算欧氏距离。 2. 曼哈顿距离(ManhattanDistance)源于纽约曼哈顿的街区结构，它忽略了坐标轴之间的角度，只考虑沿着每个坐标轴的绝对差异。在二维和n维空间中，曼哈顿距离是各坐标差的绝对值之和。Matlab同样可以利用pdist函数计算曼哈顿距离。 3. 切比雪夫距离(ChessboardDistance)是曼哈顿距离的一个特例，当所有坐标轴的权重相等时，最大坐标差即为切比雪夫距离。在n维空间中，切比雪夫距离等于向量各分量的绝对差的最大值。 4. 闵可夫斯基距离(MinkowskiDistance)是一类距离度量的总称，包括欧氏距离和曼哈顿距离作为特殊情况。它通过调整指数p来平衡各坐标轴的权重，当p=1时为曼哈顿距离，p=2时为欧氏距离。 5. 标准化欧氏距离(NormalizedEuclideanDistance)是将原始欧氏距离除以各特征的标准差，使得不同特征具有相同的尺度，常用于处理特征尺度不一致的问题。 6. 马氏距离(MahalanobisDistance)考虑了变量之间的协方差，通过协方差矩阵进行距离计算，能够识别出异常值和线性相关性。 7. 夹角余弦(CosineSimilarity)衡量两个向量的方向，而不是它们的长度，值域在-1到1之间，1表示完全相同，-1表示方向相反。 8. 汉明距离(HammingDistance)用于衡量两个等长字符串的差异，即不同位置字符的数量。 9. 杰卡德距离(JaccardDistance)和杰卡德相似系数(JaccardSimilarity)用于比较集合的相似性，基于两个集合交集和并集的比例。 10. 相关系数(CorrelationCoefficient)和相关距离(CorrelationDistance)衡量变量之间的线性相关程度，相关系数的取值范围在-1到1之间，-1表示完全负相关，1表示完全正相关。 11. 信息熵(InformationEntropy)是信息论中的概念，用于衡量信息的不确定性，可用于衡量数据集的纯度或分布的均匀性。 这些距离计算方法在机器学习中有着广泛的应用，如聚类、分类、回归等任务，选择合适的距离度量对于模型的性能至关重要。在实际应用中，需要根据数据的特性选择最合适的距离计算方法。