傅里叶变换详解：从周期信号到非周期信号

"该资源是关于信号与系统课程的第3章内容，主要讲解傅里叶变换，包括傅里叶级数分析、非周期信号的傅里叶变换、冲激函数和阶跃函数的傅里叶变换、傅里叶变换的基本性质、卷积定理、周期信号的傅里叶变换、抽样信号的傅里叶变换以及抽样定理。内容涵盖傅里叶的生平和他对信号分析的重要贡献。" 傅里叶变换是信号处理和系统分析中的核心工具，其理论源于19世纪初傅里叶的工作。在信号与系统领域，傅里叶变换是一种将信号从时域转换到频域的方法，揭示了信号的频率成分和结构。本章首先介绍了傅里叶变换的历史背景，强调了傅里叶在1807年提出的周期信号可以用正弦函数级数表示的理论，并在1822年首次发表于“热的分析理论”中。 傅里叶变换是傅里叶级数的一个扩展，适用于非周期信号。通过傅里叶变换，可以将非周期信号分解为不同频率的正弦和余弦函数的线性组合，这种表示方式被称为信号的频谱。频谱分析能够揭示信号的频率组成，如带宽、谐波和噪声成分，对于理解和设计滤波器、调制和频分复用等通信技术至关重要。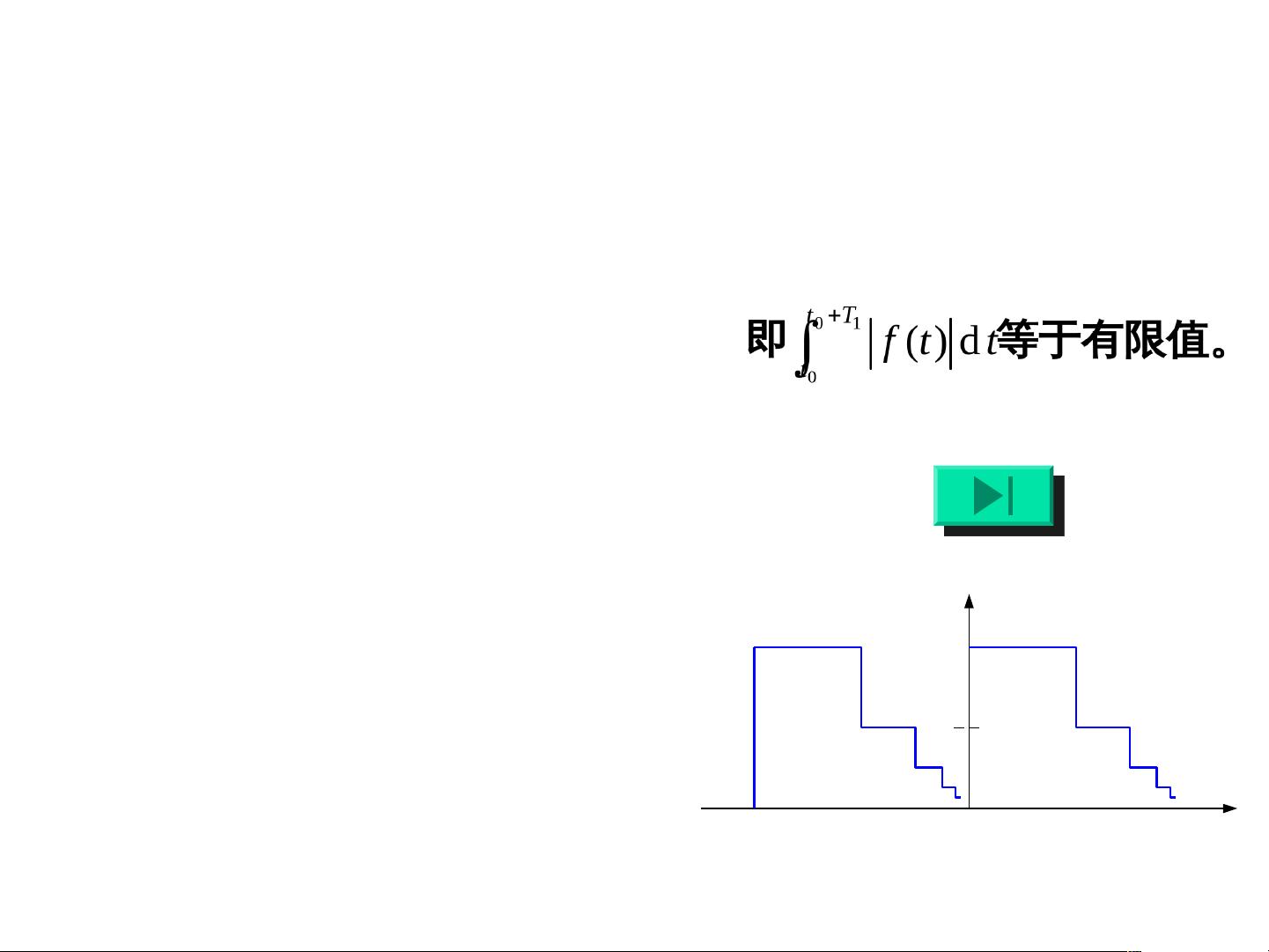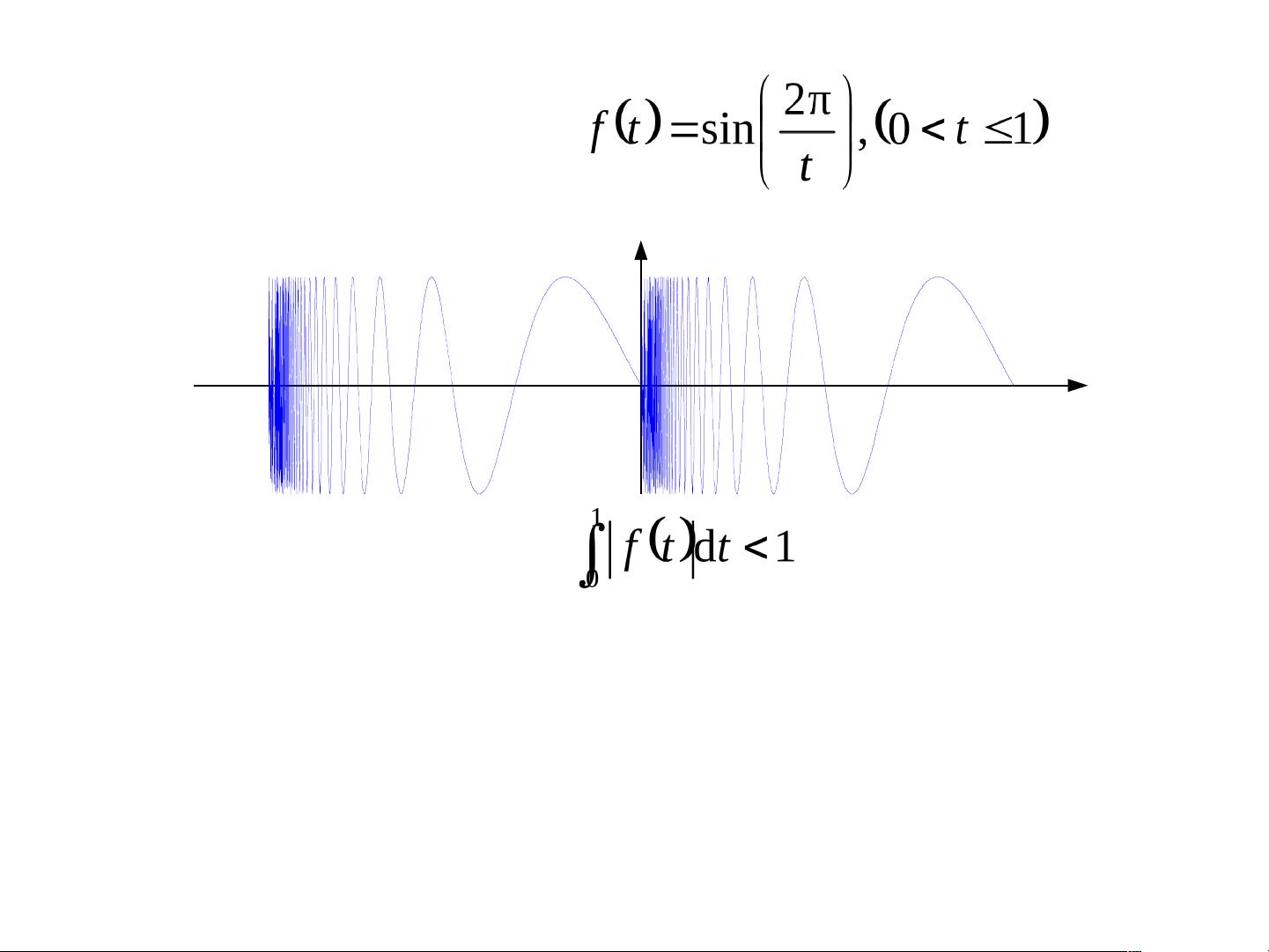 在傅里叶变换中，3.2节至3.5节详细阐述了周期信号的傅里叶级数分析和典型非周期信号的傅里叶变换。傅里叶级数适用于周期性信号，将其分解为一系列简单正弦和余弦函数的和。3.6节涉及冲激函数和阶跃函数的傅里叶变换，这两个函数在信号处理中扮演着重要角色，它们的傅里叶变换具有特殊的解析形式。 3.7节介绍了傅里叶变换的基本性质，包括线性性质、尺度变换、平移和对称性等，这些性质使得傅里叶变换在求解数学和物理问题时非常方便。3.8节的卷积定理说明了时域的卷积对应于频域的乘积，是傅里叶变换在处理线性时不变系统时的重要工具。 3.9节和3.10节分别探讨了周期信号和抽样信号的傅里叶变换。周期信号的傅里叶变换可以看作是傅里叶级数的连续版本，而抽样信号的傅里叶变换则涉及到抽样定理，这是数字信号处理的基础，它规定了保持信号信息所需的最小采样速率。 3.11节的抽样定理指出，为了无失真地恢复一个带限信号，采样频率必须至少是信号最高频率的两倍，这个原理在数字化音频和通信系统中起着关键作用。 本章深入浅出地介绍了傅里叶变换的概念、计算和应用，为理解和应用频域分析提供了坚实的基础。通过学习这一章的内容，读者可以掌握如何利用傅里叶变换分析和处理各种信号，为后续的通信系统、滤波器设计和控制系统理论的学习打下基础。