联合学习在互联与自动驾驶汽车中的应用与挑战

需积分: 5 195 浏览量更新于2024-06-13 收藏 3.01MB PDF 举报

"这篇论文是关于互联和自动化车辆在联合学习领域的应用，即Federated Learning for Connected and Automated Vehicles的调查研究。它深入探讨了如何利用机器学习（ML）技术来处理连接和自动化车辆的关键任务，如感知、规划和控制，并分析了在车辆数据用于模型训练时遇到的用户隐私和大量数据通信开销问题。文章提出了联邦学习（FL）作为一种去中心化的机器学习方法，允许多辆车协作构建模型，从而扩展从不同驾驶环境中的学习，提升整体性能，同时保护车辆本地数据的隐私和安全。" 本文主要围绕以下几个关键知识点展开： 1. **机器学习（ML）在互联和自动化车辆中的应用**：ML技术在CAV中扮演着至关重要的角色，用于车辆的感知、决策规划和控制系统，帮助车辆更好地理解环境，做出准确的行驶决策。 2. **数据隐私和通信开销问题**：在传统的集中式学习模式中，车辆数据需要上传至中央服务器进行模型训练，这可能导致用户隐私泄露且通信成本高昂，尤其是考虑到大规模的数据量。 3. **联邦学习（FL）的引入**：FL作为一种分布式机器学习策略，解决了上述问题。车辆在本地进行模型训练，只共享模型参数而非原始数据，从而保护了数据隐私，减少了通信负担。 4. **FL4CAV的主要进展**：论文回顾了FL在CAV领域的应用进展，包括算法优化、协同学习机制、隐私保护技术和通信效率的提升等方面，这些进展有助于增强CAV的智能性和安全性。 5. **挑战与未来方向**：文章还讨论了FL在CAV实施中面临的挑战，如异构性、动态网络环境、延迟问题以及对实时性的要求等，并展望了未来的研究方向，包括强化FL的适应性和鲁棒性，以及在CAV领域的进一步应用。这篇调查论文全面分析了FL在互联和自动化车辆中的潜力和局限性，为该领域的研究人员提供了有价值的参考，推动了智能交通系统的发展，同时也对保护用户隐私和提升系统效率提出了新的解决方案。

122 IEEE TRANSACTIONS ON INTELLIGENT VEHICLES, VOL. 9, NO. 1, JANUARY 2024

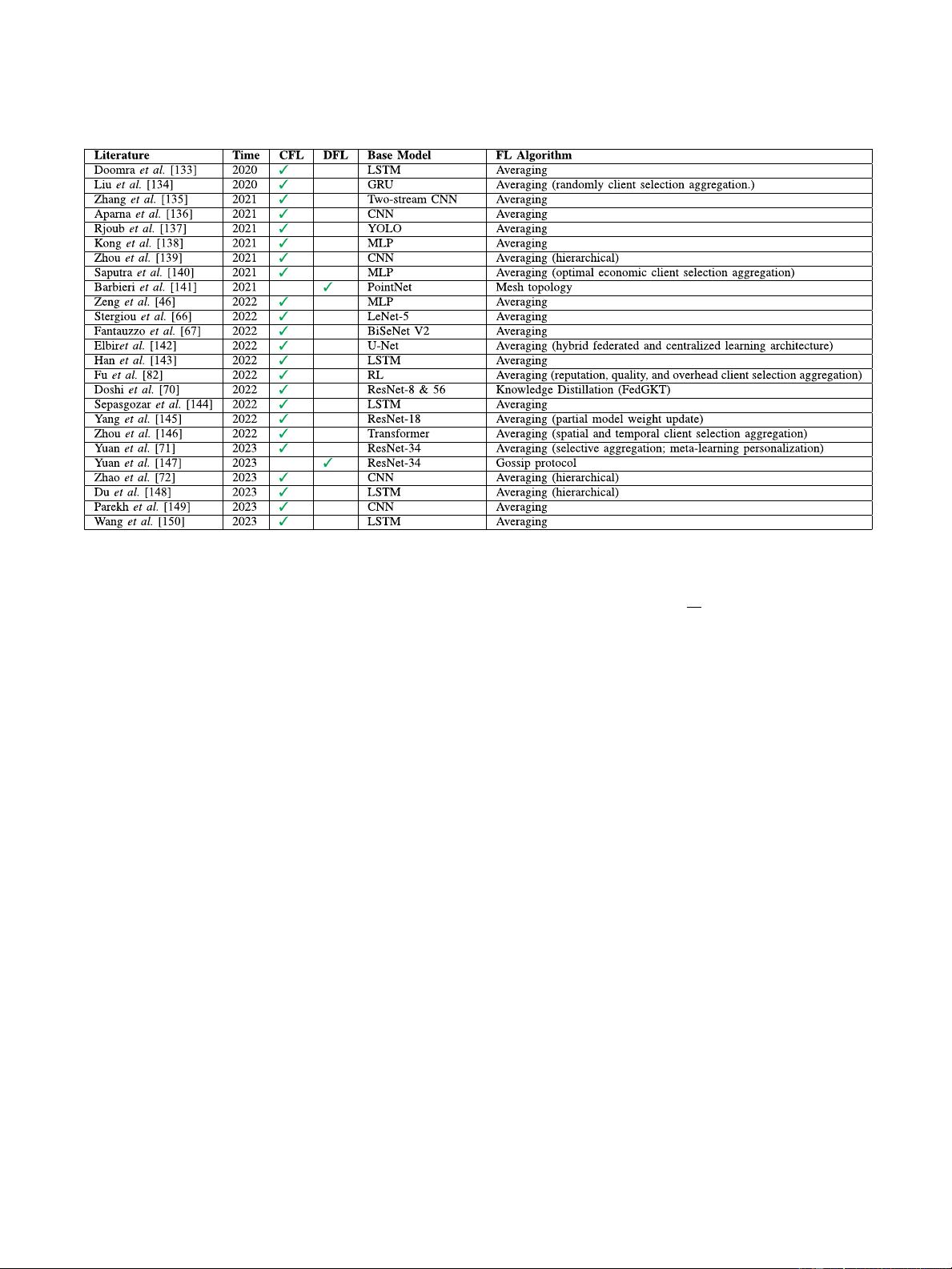
TABLE III

ITERATURE OVERVIEW OF FL FOR CAV ALGORITHMS

This training process typically adopts a simple Stochastic

Gradient Descent (SGD) algorithm. The computational

infrastructure is usually limited.

3) Local Update Upload: After training the model, each ve-

hicle applies privacy-preserving techniques such as differ-

ential privacy (introduces artiﬁcial noise to the parameters)

and then uploads/communicates the model parameters to

the selected central server (Centralized Federated Learn-

ing, i.e., CFL) or other vehicles (Decentralized Federated

Learning, i.e., DFL).

4) Aggregation of Vehicle Updates: The server securely ag-

gregates the parameters uploaded from K vehicles to

obtain the global model. Furthermore, it tests the model’s

performance.

A. Centralized Federated Learning

In this section, we review two major aggregation methods in

the centralized framework, namely averaging and a more recent

technique called knowledge distillation.

1) Averaging: Most of the existing literature uses the Feder-

ated Averaging (FedAvg) algorithm [25] for the FL aggregation

process on the server—see Table III. FedAvg applies SGD op-

timization to local vehicles and performs a weighted averaging

of the weights of the vehicles on the central server. FedAvg

performs multiple local gradient updates before s ending the

parameters to the server, reducing the number of communication

rounds. For FL4CAV, data on each CAV are dynamically updated

at each communication round.

A typical FL setup has K vehicles that have their own local

data sets and the ability to perform simple local optimization. At

the central server, the optimization problem can be represented

min

x∈R



f(x)=



i=1

)



, (1)

where f

: R

→ R for i ∈{1,...,K} is the local objective

function of the ith vehicle. The local objective function of the

ith vehicle can have the form,

)=E

∼D

[(x

,ξ

)], (2)

where ξ

represents the data that have been sampled from the

local vehicle data D

for the i

vehicle. The expectation oper-

ator, E, is acting on the local objective function, (x

,ξ

),with

respect to a data sample, ξ

, drawn from the vehicle data, D

The function (x

,ξ

) is the loss function evaluated for each

vehicle, x

, and data sample, ξ

. Here, x

∈ R

represents the

model parameters of vehicle i, and X ∈ R

d×K

is the matrix

formed using these parameter vectors. The learning process

is performed to ﬁnd a minimizer of the objective function,

= x

∗

=argmin

x∈R

f(x).

The data obtained from CAVs are typically non-independent

and non-identically distributed (non-IID). FedAvg faces chal-

lenges in realistic heterogeneous data settings, as a single global

model may not perform well for individual vehicles, and mul-

tiple local updates can cause the updates to deviate from the

global objective [44]. Several variants of FedAvg have been

proposed to address the challenges encountered by FL, such

as data heterogeneity, client drift, local vehicle data imbalance,

communication latency, and computation capabilities. FedProx

algorithm, FedAvg with a proximal term, has been proposed to

improve the convergence and reduce communication cost [45].

Dynamic Federated Proximal [46] algorithm (DFP) is an exten-

sion of FedProx that could effectively deal with non-IID data

Authorized licensed use limited to: Zhengzhou University. Downloaded on April 27,2024 at 09:15:34 UTC from IEEE Xplore. Restrictions apply.

剩余18页未读，继续阅读

yuan_0012

粉丝: 9
资源: 6

联合学习在互联与自动驾驶汽车中的应用与挑战

基于Matlab的联合学习仿真：高效沟通的代码实践

联合学习：在分布式数据上高效训练深度网络

电力AI竞赛：安全帽未佩戴行为检测基准模型

综述1-Federated Learning for Computer Vision

ReputationBased-Regional-Federated-Learning-for-Knowledge-Tradin

2018-FL+可靠的低通耗网络-Federated Learning for Ultra-Reliable Low-Laten

Multi-Armed-Bandit-Based-Client-Scheduling-for-Federated-Learning:联合学习中基于多武装强盗的客户调度文章中的代码隐含

SSFL-Benchmarking-Semi-supervised-Federated-Learning:对标半监督联合学习

Blockchain-Federated-Learning and Deep Learning.pdf

awesome-federated-learning:机器学习中有关联合学习和隐私的资源

最新资源