可逆循环神经网络：降低训练内存需求的新途径

需积分: 10 193 浏览量更新于2024-07-16 收藏 2.25MB PDF 举报

"这篇论文探讨了可逆循环神经网络(Reversible Recurrent Neural Networks)在处理序列数据时如何降低训练过程中的内存需求。通过允许隐藏层到隐藏层的转换可以逆转，可逆RNN旨在减少训练期间必须存储的隐藏状态，从而在反向传播过程中重新计算这些状态。然而，作者指出，完全可逆的RNN存在限制，因为它们无法从隐藏状态中遗忘信息。为了克服这个问题，他们提出了一种方法，即在隐藏状态中存储少量位，以实现遗忘的同时保持可逆性。这种方法在保持与传统模型相当的性能下，降低了激活内存成本，减少了10到15倍。此外，该技术也被扩展到基于注意力的序列到序列模型中，在编码器中减少了5到10倍的激活内存成本，而在解码器中减少了10到15倍。" 可逆循环神经网络（RNN）是循环神经网络的一个变体，其核心思想是使得网络的前向传播过程能够被逆转。这在理论上允许在反向传播时重算隐藏状态，而不是保存这些状态，从而显著减少了内存消耗。然而，一个完全可逆的RNN存在一个关键问题：由于其不能遗忘旧的信息，它可能无法适应长期依赖问题，这是许多RNN遇到的挑战。为了解决这个问题，研究者提出了一个策略，即在隐藏状态中保留少量的位，以允许网络在保持可逆性的同时遗忘不重要的信息。这种方法在实践中证明是有效的，因为它能够在不牺牲性能的前提下，显著降低训练过程中的激活内存需求。在与传统RNN模型的比较中，这种可逆RNN方法成功地实现了内存成本的10到15倍的减少。此外，这种技术也被应用于基于注意力的序列到序列模型。在这些模型中，编码器和解码器通常需要处理大量的上下文信息，因此内存效率尤其重要。应用可逆RNN的方法后，编码器的激活内存成本降低了5到10倍，解码器则降低了10到15倍。这样的改进对于处理长序列和复杂语言任务的自然语言处理（NLP）模型来说，是一个巨大的进步，因为它不仅保持了模型的性能，还显著提升了训练效率。可逆RNN提供了一个创新的解决方案，通过引入有限的遗忘能力，克服了完全可逆网络的局限性，同时大幅度减少了内存使用，这对于大规模NLP任务的训练具有重大意义。这一研究成果为未来优化RNN训练过程和提高资源利用效率打开了新的可能性。

...

Attention

...

<SOS>

DecoderEncoder

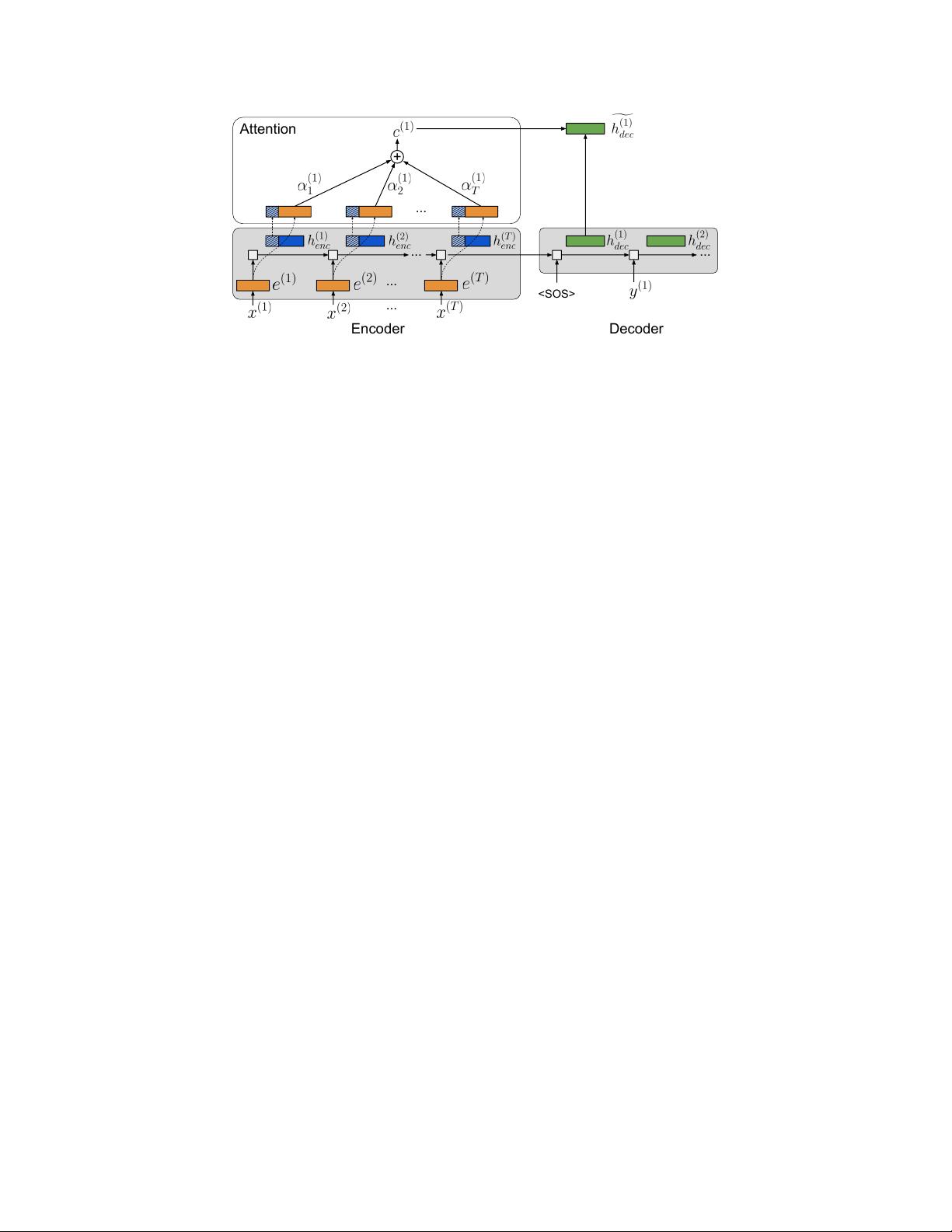
Figure 2:

Attention mechanism for NMT.

The word embeddings, encoder hidden states, and decoder hidden

states are color-coded orange, blue, and green, respectively; the striped regions of the encoder hidden states

represent the slices that are stored in memory for attention. The ﬁnal vectors used to compute the context vector

are concatenations of the word embeddings and encoder hidden state slices.

5.1 GPU Considerations

For our method to be used as part of a practical training procedure, we must run it on a parallel

architecture such as a GPU. This introduces additional considerations which require modiﬁcations to

Algorithm 1: (1) we implement it with ordinary ﬁnite-bit integers, hence dealing with overﬂow, and

(2) for GPU efﬁciency, we ensure uniform memory access patterns across all hidden units.

Overﬂow.

Consider the storage required for a single hidden unit. Algorithm 1 assumes unboundedly

large integers, and hence would need to be implemented using dynamically resizing integer types,

as was done by Maclaurin et al.

[13]

. But such data structures would require non-uniform memory

access patterns, limiting their efﬁciency on GPU architectures. Therefore, we modify the algorithm

to use ordinary ﬁnite integers. In particular, instead of a single integer, the buffer is represented

with a sequence of 64-bit integers

, . . . , B

)

. Whenever the last integer in our buffer is about to

overﬂow upon multiplication by

, as required by step 1 of Algorithm 1, we append a new integer

D+1

to the sequence. Overﬂow will occur if B

> 2

64−R

After appending a new integer

D+1

, we apply Algorithm 1 unmodiﬁed, using

D+1

in place of

It is possible that up to

−1

bits of

will not be used, incurring an additional penalty on storage

cost. We experimented with several ways of alleviating this penalty but found that none improved

signiﬁcantly over the storage cost of the initial method.

Vectorization.

Vectorization imposes an additional penalty on storage. For efﬁcient computation,

we cannot maintain different size lists as buffers for each hidden unit in a minibatch. Rather, we must

store the buffer as a three-dimensional tensor, with dimensions corresponding to the minibatch size,

the hidden state size, and the length of the buffer list. This means each list of integers being used as a

buffer for a given hidden unit must be the same size. Whenever a buffer being used for any hidden

unit in the minibatch overﬂows, an extra integer must be added to the buffer list for every hidden unit

in the minibatch. Otherwise, the steps outlined above can still be followed.

We give the complete, revised algorithm in Appendix C.3. The compromises to address overﬂow and

vectorization entail additional overhead. We measure the size of this overhead in Section 6.

5.2 Memory Savings with Attention

Most modern architectures for neural machine translation make use of attention mechanisms [

];

in this section, we describe the modiﬁcations that must be made to obtain memory savings when

using attention. We denote the source tokens by

(1)

, x

(2)

, . . . , x

(T )

, and the corresponding word

embeddings by

(1)

, e

(2)

, . . . , e

(T )

. We also use the following notation to denote vector slices: given

a vector

v ∈ R

, we let

v[: k] ∈ R

denote the vector consisting of the ﬁrst

dimensions of

Standard attention-based models for NMT perform attention over the encoder hidden states; this is

problematic from the standpoint of memory savings, because we must retain the hidden states in

memory to use them when computing attention. To remedy this, we explore several alternatives to

storing the full hidden state in memory. In particular, we consider performing attention over: 1) the

embeddings

(t)

, which capture the semantics of individual words; 2) slices of the encoder hidden

Table 1: Validation perplexities (memory savings) on Penn TreeBank word-level language modeling. Results

shown when forgetting is restricted to

, and

bits per hidden unit per timestep and when there is no restriction.

Reversible Model 2 bit 3 bits 5 bits No limit Usual Model No limit

1 layer RevGRU 82.2 (13.8) 81.1 (10.8) 81.1 (7.4) 81.5 (6.4) 1 layer GRU 82.2

2 layer RevGRU 83.8 (14.8) 83.8 (12.0) 82.2 (9.4) 82.3 (4.9) 2 layer GRU 81.5

1 layer RevLSTM 79.8 (13.8) 79.4 (10.1) 78.4 (7.4) 78.2 (4.9) 1 layer LSTM 78.0

2 layer RevLSTM 74.7 (14.0) 72.8 (10.0) 72.9 (7.3) 72.9 (4.9) 2 layer LSTM 73.0

states,

(t)

enc

[: k]

(where we consider

k = 20

100

); and 3) the concatenation of embeddings and

hidden state slices,

(t)

; h

(t)

enc

[: k]]

. Since the embeddings are computed directly from the input

tokens, they don’t need to be stored. When we slice the hidden state, only the slices that are attended

to must be stored. We apply our memory-saving buffer technique to the remaining

D −k

dimensions.

In our NMT models, we make use of the global attention mechanism introduced by Luong et

al. [

], where each decoder hidden state

(t)

dec

is modiﬁed by incorporating context from the source

annotations: a context vector

(t)

is computed as a weighted sum of source annotations (with weights

(t)

);

(t)

dec

and

(t)

are used to produce an attentional decoder hidden state

(t)

dec

. Figure 2 illustrates

this attention mechanism, where attention is performed over the concatenated embeddings and hidden

state slices. Additional details on attention are provided in Appendix F.

5.3 Additional Considerations

Restricting forgetting.

In order to guarantee memory savings, we may restrict the entries of

(t)

to lie in

(a, 1)

rather than

(0, 1)

, for some

a > 0

. Setting

a = 0.5

, for example, forces our model to

forget at most one bit from each hidden unit per timestep. This restriction may be accomplished by

applying the linear transformation x 7→ (1 − a)x + a to z

(t)

after its initial computation

Limitations.

The main ﬂaw of our method is the increased computational cost. We must reconstruct

hidden states during the backwards pass and manipulate the buffer at each timestep. We ﬁnd that

each step of reversible backprop takes about 2-3 times as much computation as regular backprop. We

believe this overhead could be reduced through careful engineering. We did not observe a slowdown

in convergence in terms of number of iterations, so we only pay an increased per-iteration cost.

6 Experiments

We evaluated the performance of reversible models on two standard RNN tasks: language modeling

and machine translation. We wished to determine how much memory we could save using the

techniques we have developed, how these savings compare with those possible using an idealized

buffer, and whether these memory savings come at a cost in performance. We also evaluated our

proposed attention mechanism on machine translation tasks.

6.1 Language Modeling Experiments

We evaluated our one- and two-layer reversible models on word-level language modeling on the Penn

Treebank [

] and WikiText-2 [

] corpora. In the interest of a fair comparison, we kept architectural

and regularization hyperparameters the same between all models and datasets. We regularized the

hidden-to-hidden, hidden-to-output, and input-to-hidden connections, as well as the embedding

matrix, using various forms of dropout

. We used the hyperparameters from Merity et al.

[3]

. Details

are provided in Appendix G.1. We include training/validation curves for all models in Appendix I.

6.1.1 Penn TreeBank Experiments

We conducted experiments on Penn TreeBank to understand the performance of our reversible models,

how much restrictions on forgetting affect performance, and what memory savings are achievable.

Performance.

With no restriction on the amount forgotten, one- and two-layer RevGRU and

RevLSTM models obtained roughly equivalent validation performance

compared to their non-

For the RevLSTM, we would apply this transformation to p

(t)

and f

(t)

We discuss why dropout does not require additional storage in Appendix E.

Test perplexities exhibit similar patterns but are 3–5 perplexity points lower.

剩余30页未读，继续阅读

hywcxq

粉丝: 0
资源: 33

可逆循环神经网络：降低训练内存需求的新途径

Reversible-Column-Networks优化YOLOv7检测电动车头盔佩戴

Reversible-Column-Networks改进YOLOv7的电动车头盔检测系统

JavaScript可逆随机数生成器：利用线性同余算法

Reversible Struc省略 Thulium Anions.pdf

可逆水印.pdf 可逆水印.pdf

论文研究-Design of a Reversible Data Hiding Algorithm Based on Dynamic DC-QIM.pdf

Google C++ International Standard.pdf

数学模型 Lecture Notes.pdf

HSL抗体说明书图解.pdf

自动聚类算法确定cluster数目的方法.pdf

最新资源