Matlab实现Koch分形与基本步骤解析

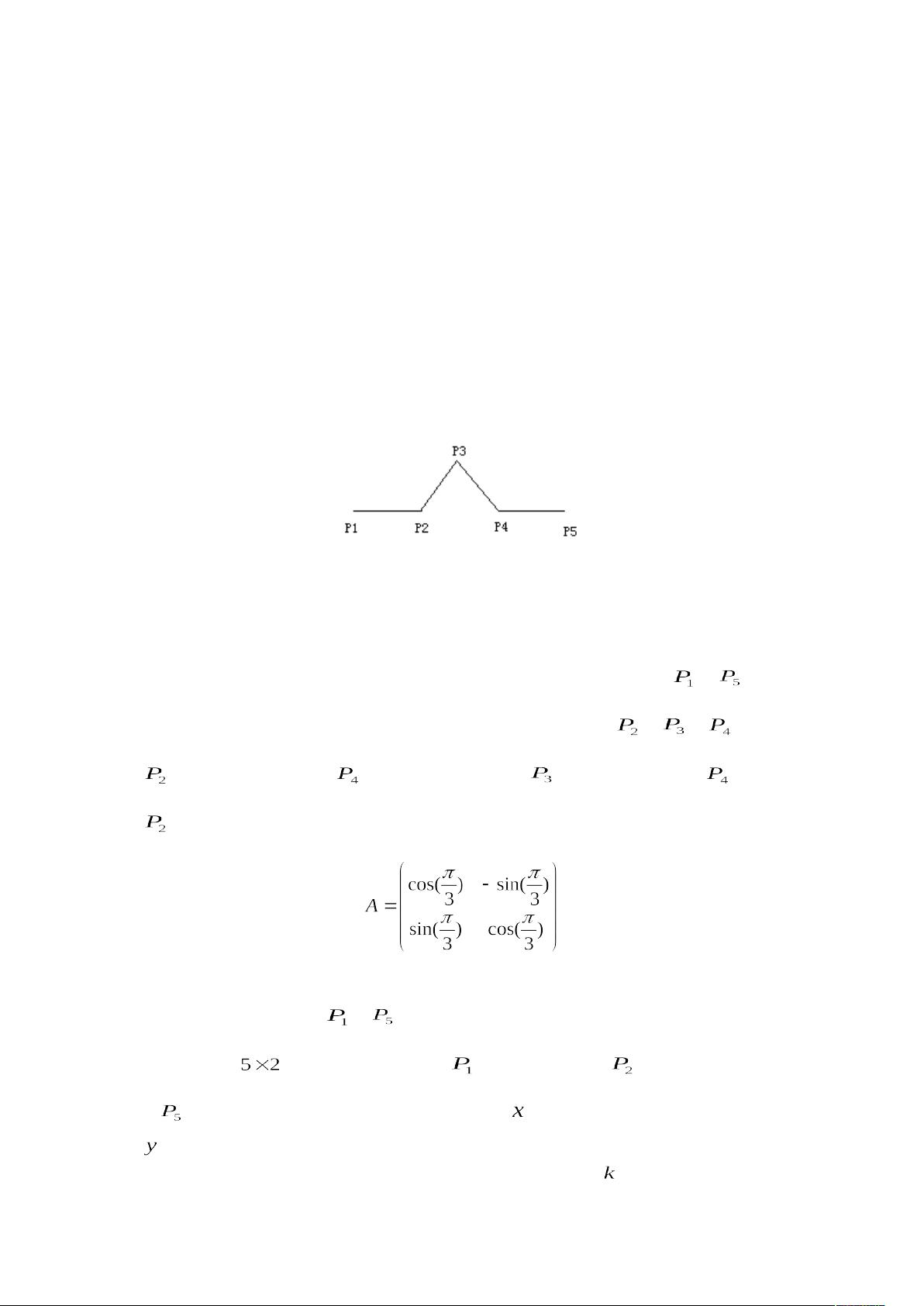
在MATLAB中实现几个分形图形的示例，以Koch曲线为例进行深入解析。Koch曲线是一种典型的自相似分形几何结构，它通过不断复制和变形简单的形状来生成复杂的图形。在这个实例中，我们首先定义了初始的两个点坐标p=[0 0;10 0]，其中n=2表示当前的节点数量。接下来，使用旋转矩阵A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]进行30度的逆时针旋转，这是构建Koch曲线的关键步骤。 算法的核心是每次迭代都将每个线段分成三等分，取中间部分并用等边三角形连接。在第一次迭代中，会增加3个新点，使得原来的2个点变为5个。在后续的迭代中，每次增加的数量是前一次的4倍减去3，即m=4n-3。例如，第二次迭代时，结点数为5*4-3=17，第三次为17*4-3=65，以此类推。 程序中，diff函数用于计算相邻两点之间的向量，并将其长度除以3，表示分割后的向量长度。通过这个过程，我们可以动态地更新点的坐标，生成Koch曲线的各个阶段。在循环(k=1:4)中，分别处理不同位置的点，如原点附近的点(p(1:n-1,:))保持不变，而其他点则是根据迭代公式和向量操作进行更新。 总结来说，这个MATLAB代码展示了如何通过迭代和几何变换来构造Koch曲线，以及如何利用矩阵操作来管理节点坐标。理解并实现这种分形图案不仅有助于深入理解数学美学，还能够提升编程技能，尤其是在处理几何和动态结构的场景中。通过实践，可以扩展到其他分形，如Sierpinski三角形或Mandelbrot集合，进一步探索计算机图形学中的复杂之美。