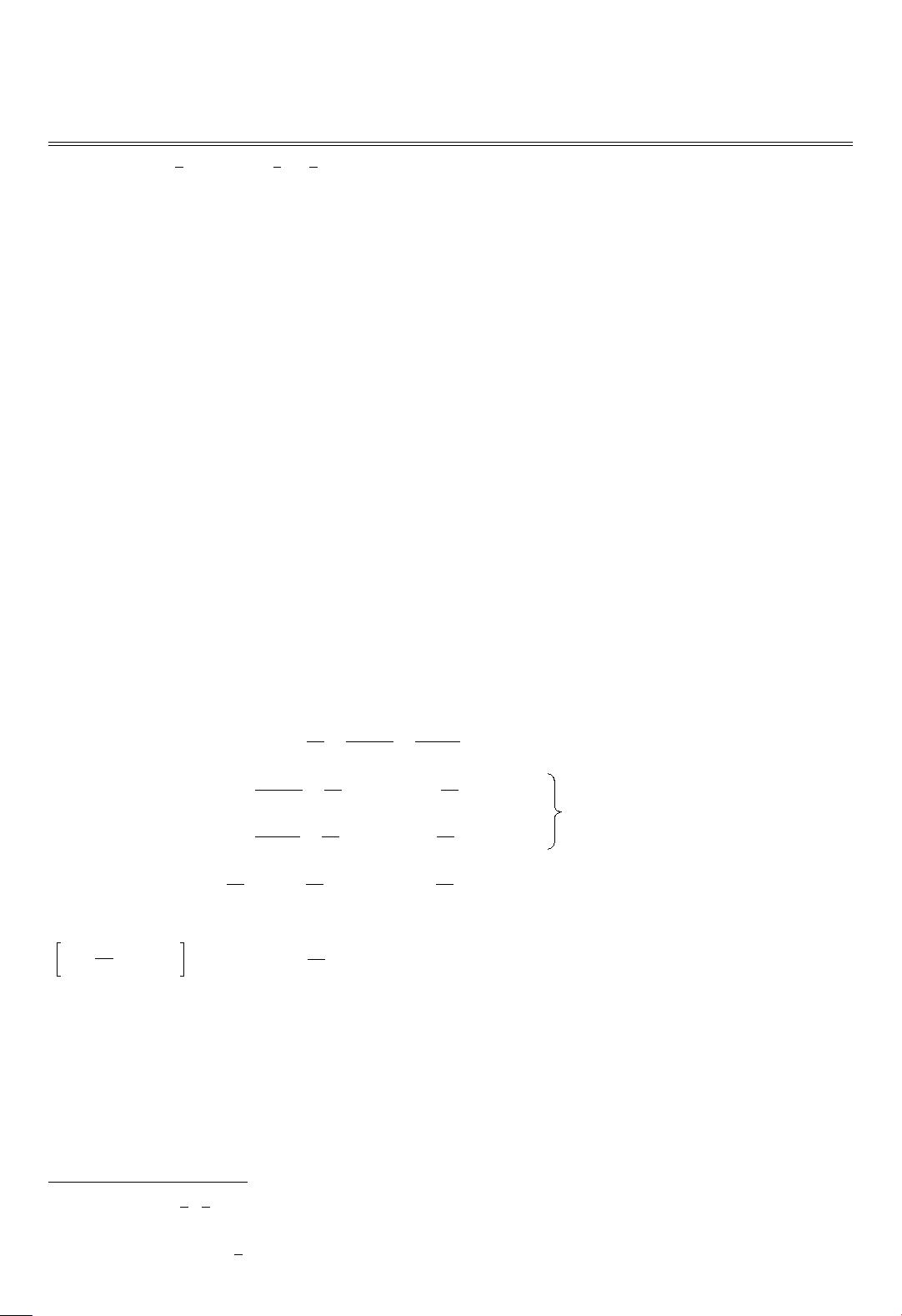2+1维欧拉方程对称约化与优化系统：新方法与显式解

本文主要探讨了(2+1)维欧拉方程组在物理学中的重要地位，特别是流体力学中的模型。欧拉方程组是一类非线性偏微分方程，它广泛应用于描述各种复杂的物理现象，如气体动力学、液体流动等。对于这类方程组求解的精确解具有深远的理论价值和实际应用意义。 作者利用经典李群方法，深入分析了(2+1)维欧拉方程组的不变群性质，这是理解方程对称性的关键步骤。通过不变群的探讨，作者揭示了方程组的对称性和群不变解，这些解提供了解决问题的一种新视角。对称性的应用不仅有助于简化方程，还可能导致新的显式解的发现，这在数值计算和理论研究中都是极具价值的进展。 文中提到了一些已有的求解欧拉方程的有效方法，例如达布罗夫变换法、贝克隆德变换法以及数值模拟技术（如有限差分法、有限体积元法和谱方法）。然而，本文关注的是通过直接对称方法来处理欧拉方程组，这是一种独特且有力的解决策略。 具体到(2+1)维欧拉方程组（1），它包括质量守恒、动量守恒和能量守恒三个方程，涉及到密度、流速以及能量等物理量。通过对称约化，作者能够将这个复杂系统转化为更易于处理的形式，从而可能找到新的解析解或者简化数值求解的过程。 这篇文章不仅深化了我们对(2+1)维欧拉方程组对称特性的理解，而且为求解此类方程提供了一种新颖且有效的途径，这对于推进流体力学的研究以及实际工程问题的数值模拟具有重要的学术价值。