基于仿射算法的分布式估计算法研究
需积分: 10 100 浏览量
更新于2024-09-11
收藏 2.3MB PDF 举报
"分布式估计算法基于仿射算法的研究"
分布式估计算法是指在分布式系统中实现参数估计算法的方法。该方法可以应用于各个领域，如信号处理、图像处理、机器学习等。分布式估计算法的优点在于可以充分利用分布式系统的计算资源，提高计算速度和准确性。
分布式估计算法基于仿射算法的研究是指使用仿射算法来实现分布式估计算法。仿射算法是一种常用的优化算法，可以用来解决非线性最小二乘问题。在分布式估计算法中，仿射算法可以用来更新每个节点的参数，从而实现分布式估计算法。
本文提出了一种基于仿射算法的分布式估计算法，该算法可以在 adaptive incremental network 中实现分布式估计算法。该算法可以克服传统的 least-mean-square (LMS) 类型的分布式自适应滤波器的收敛性问题，实现更快的收敛速度和更好的稳态性能。
在该算法中，每个节点都可以独立地更新自己的参数，而不需要与其他节点进行通信。这种方式可以大大提高计算速度和准确性。同时，该算法也可以很好地适应 colored inputs，即输入信号具有色彩特性的情况。
在该文中，作者们还提出了一个基于 weighted spatial-temporal energy conservation relation 的分析方法来分析算法的暂态和稳态性能。该方法可以很好地描述算法的收敛过程和稳态性能。
通过计算机仿真，作者们验证了该算法的有效性。结果表明，该算法可以提供更快的收敛速度和更好的稳态性能，相比于 LMS 基础的方案。此外，该算法还可以实现可接受的 misadjustment 性能。
本文提出的分布式估计算法基于仿射算法的研究可以为分布式系统的参数估计提供了一种有效的方法。该方法可以应用于各个领域，提高计算速度和准确性。
知识点：
1. 分布式估计算法是指在分布式系统中实现参数估计算法的方法。
2. 仿射算法是一种常用的优化算法，可以用来解决非线性最小二乘问题。
3. 分布式估计算法基于仿射算法的研究可以克服传统的 LMS 类型的分布式自适应滤波器的收敛性问题。
4. 该算法可以在 adaptive incremental network 中实现分布式估计算法。
5. 该算法可以实现更快的收敛速度和更好的稳态性能。
6. 该算法可以很好地适应 colored inputs，即输入信号具有色彩特性的情况。
7. Weighted spatial-temporal energy conservation relation 可以用来分析算法的暂态和稳态性能。
8. 该算法可以提供更快的收敛速度和更好的稳态性能，相比于 LMS 基础的方案。
9. 该算法还可以实现可接受的 misadjustment 性能。
本文提出的分布式估计算法基于仿射算法的研究可以为分布式系统的参数估计提供了一种有效的方法。该方法可以应用于各个领域，提高计算速度和准确性。
LI et al.: DISTRIBUTED ESTIMATION OVER AN ADAPTIVE INCREMENTAL NETWORK 153
global estimation at time instant . Consider a Newton’s search
based approach to solving (9) for incremental learning within
a distributed network. The optimal tap weight
is estimated
via [17]
(10)
where
, , denotes a regu-
larization parameter with small positive value,
indicates
an appropriately chosen step-size, which is evaluated in
Section III-E, and the scheme is initialized with an
1
vector
.
For a practical scheme to realize (10), and utilizing the corre-
lation of the input signal at each node, we replace
by the following sample sliding-window estimates:
(11)
(12)
with
equal to the number of recent regressors of each node
whilst
and denote the corresponding input vector and
desired response at instant time
for the th node. Hence, using
the matrix inversion formula, recursion (10) becomes,
(13)
where the local
block data matrix and 1 data vector
are
.
.
.
.
.
.
(14)
and
is employed to avoid the inversion of a rank deficient ma-
trix
. As such, recursion (13) is the distributed APA
(dAPA) learning algorithm in an incremental network, the op-
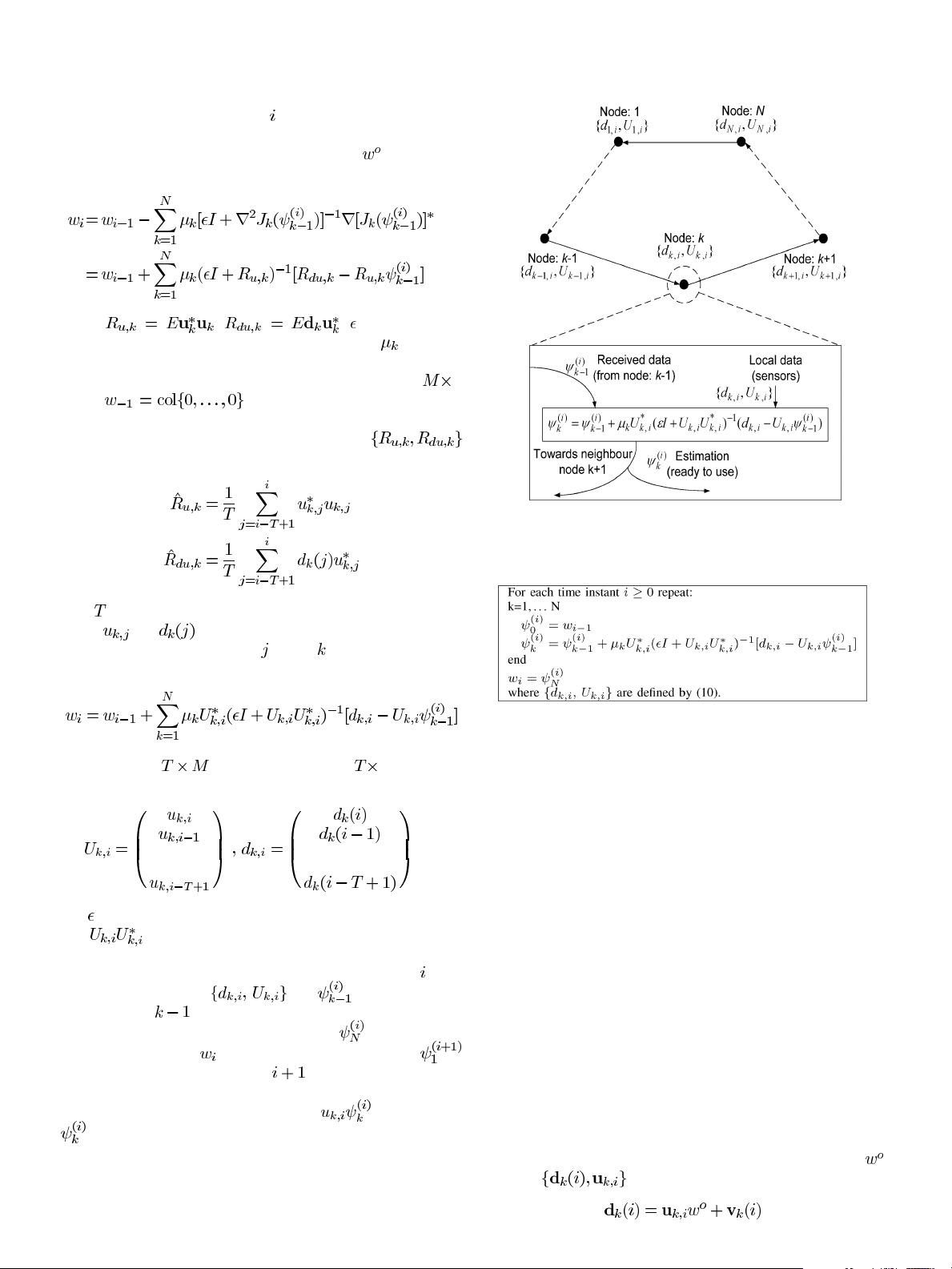
eration of which is shown in Fig. 1. At each time instant
, each
node utilizes local data
and received from its
previous node
in the cycle to update the local estimation.
At the end of the cycle, the local estimation
is employed as
the global estimation and the initial local estimation
for the next discrete time instant . The final weight vector
shown at the bottom of Fig. 1 can either be used to generate
a filter output vector term of the form
or the vector
itself can then be used for system identification or equaliza-
tion. The pseudo-code implementation of dAPA is described in
Table I. In addition, dAPA has intermediate computational and
memory cost between dLMS and dRLS, for certain regressor
length, which is verified in the Appendix.
Fig. 1. Data processing of the dAPA algorithm in an incremental network.
TABLE I
P
SEUDO-CODE IMPLEMENTATION OF D
APA
III. PERFORMANCE ANALYSIS
The convergence behaviors of classical APA-based algo-
rithms are studied in [15]–[19], exploiting arguments based on
a single adaptive filter. In order to study the performance of the
dAPA algorithm, we extend the weighted energy conservation
approach for the APA-based algorithms of [18], [19] to the
case of a distributed incremental network, which involves both
the space dimension and the time dimension. However, due to
the energy flow across the interconnected filter, some of the
simplifications for a single filter case cannot be adopted. A
set of weighting matrices is particularly chosen to decouple a
set of equations and we evaluate the transient and steady-state
performances at each individual node in terms of mean-square
deviation (MSD), excess mean-square-error (EMSE) and
mean-square error (MSE). The closed-form expressions for
the theoretical results are formed under some simplifying
assumptions described below.
A. Data Model and Assumption
As defined earlier, we use boldface letters as the random
quantities and assume the same model as in [9] to carry out the
performance analysis:
A1) The relation between the unknown system vector
and takes the form:
(15)
剩余13页未读，继续阅读
2021-02-07 上传
2021-05-30 上传
2021-05-11 上传
2021-02-10 上传
188 浏览量
386 浏览量
108 浏览量
2021-02-21 上传
2021-01-20 上传
2021-02-10 上传
164921697
- 粉丝: 0
- 资源: 6
我的内容管理
展开
