隐马尔可夫模型(HMM)教程:理解与应用
需积分: 10 153 浏览量
更新于2024-07-23
收藏 647KB PDF 举报
"HMM学习最佳范例"
在学习隐马尔科夫模型(Hidden Markov Model,简称HMM)时,我们关注的核心是通过观察序列来理解隐藏状态的序列。HMM是一种统计建模方法,广泛应用于自然语言处理、生物信息学、语音识别等领域,因为它能够处理观察数据和潜在状态之间的不完全对应问题。
一、HMM的基本概念
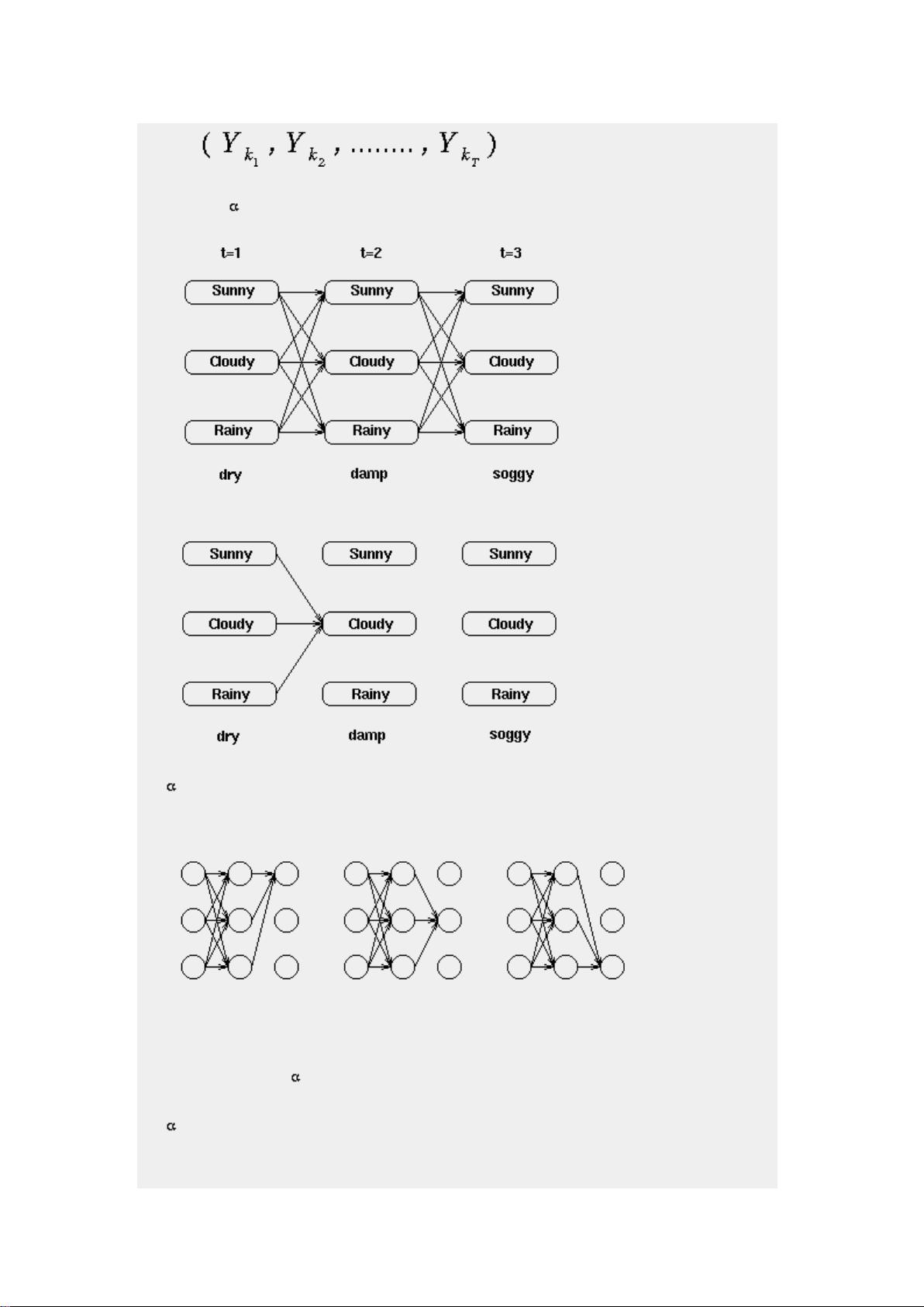
HMM由两个主要部分组成:状态和观测。状态是不可见的,只能间接通过观测来推断;观测是可以直接获取的数据,它们是由当前状态产生的。在天气预测的例子中,状态可以是“晴天”、“雨天”或“多云”,而观测是海藻的“湿透”、“干燥”或“有湿气”。
二、HMM的三个基本问题
1. **生成模式(Generation)**:给定模型参数,HMM可以生成符合其状态转移和观测概率的随机序列。例如,根据特定的天气状态转移概率和海藻状态对应的天气概率,我们可以生成一个模拟的海藻状态序列。
2. **学习问题(Learning)**:在已知观测序列的情况下,我们需要估计出最能解释这些观测的HMM参数。这通常通过贝叶斯方法或最大似然估计来实现,如Baum-Welch算法。
3. **解码问题(Decoding)**:给定观测序列,找到最可能对应的一系列隐藏状态,即Viterbi解码。例如,如果我们知道一周的海藻状态,我们想找出最可能的天气序列。
三、HMM的状态转移和观测概率
1. **状态转移概率**(A矩阵):定义了从一个状态转移到另一个状态的概率。在天气模型中,这表示从“晴天”到“雨天”的概率、从“雨天”到“晴天”的概率等。
2. **观测概率**(B矩阵):定义了每个状态产生特定观测的概率。在海藻的例子中,这表示“晴天”下海藻“干燥”的概率、“雨天”下海藻“湿透”的概率等。
四、 Baum-Welch算法和维特比算法
Baum-Welch算法用于解决学习问题,通过迭代优化模型参数,使得观测序列的似然性最大化。维特比算法则用于解码问题,通过动态规划找到最有可能的隐藏状态序列。
五、应用实例
HMM可以用来解决多种实际问题,如词性标注、语音识别、基因定位等。在天气预报的场景中,我们不仅可以预测未来天气,还可以通过历史观测推断季节,比如连续的“干燥”状态可能指示夏季,而连续的“湿透”状态可能代表冬季。
HMM提供了一种强大的工具,让我们能够在只看到部分信息的情况下,去推测完整的系统行为。通过对HMM的理解和应用,我们可以解决许多现实世界中存在不确定性和部分可观测性的复杂问题。
2009-09-22 上传
2011-04-05 上传
2012-08-08 上传
2023-05-27 上传
2024-08-25 上传
2024-01-06 上传
2023-09-06 上传
2023-08-01 上传
2024-01-10 上传
WangLanguager
- 粉丝: 1w+
- 资源: 300
最新资源
- Angular程序高效加载与展示海量Excel数据技巧
- Argos客户端开发流程及Vue配置指南
- 基于源码的PHP Webshell审查工具介绍
- Mina任务部署Rpush教程与实践指南
- 密歇根大学主题新标签页壁纸与多功能扩展
- Golang编程入门:基础代码学习教程
- Aplysia吸引子分析MATLAB代码套件解读
- 程序性竞争问题解决实践指南
- lyra: Rust语言实现的特征提取POC功能
- Chrome扩展:NBA全明星新标签壁纸
- 探索通用Lisp用户空间文件系统clufs_0.7
- dheap: Haxe实现的高效D-ary堆算法
- 利用BladeRF实现简易VNA频率响应分析工具
- 深度解析Amazon SQS在C#中的应用实践
- 正义联盟计划管理系统:udemy-heroes-demo-09
- JavaScript语法jsonpointer替代实现介绍