动态规划状态压缩解析：位运算与递推解法

"这篇资料主要介绍了动态规划中的状态压缩技巧，通过PPT的形式进行讲解。动态规划有时状态复杂，状态压缩能用简洁方式表示。常用方法是用二进制整数表示状态集合。资料提到了位运算在状态压缩中的应用，并以一个简单的棋盘放置车的问题为例，解释如何运用状态压缩进行递推解题。" 动态规划是一种解决最优化问题的有效方法，但在处理涉及大量状态的问题时，状态表示和状态转移可能会变得非常复杂。状态压缩是一种处理这种复杂性的策略，尤其适用于当状态可以用一个集合来描述，而集合的元素可以通过二进制位来表示的情况。例如，如果一个状态由多个布尔值组成，可以用一个整数的二进制表示来代替，其中每一位对应一个布尔值。 位运算是状态压缩的核心工具，包括NOT（按位非）、AND（按位与）、OR（按位或）和XOR（按位异或）。在动态规划中，这些操作可以用来高效地处理和转换状态。例如，AND操作可以用于取出一个数的特定二进制位，而XOR操作可以用于在不使用中间变量的情况下交换两个数。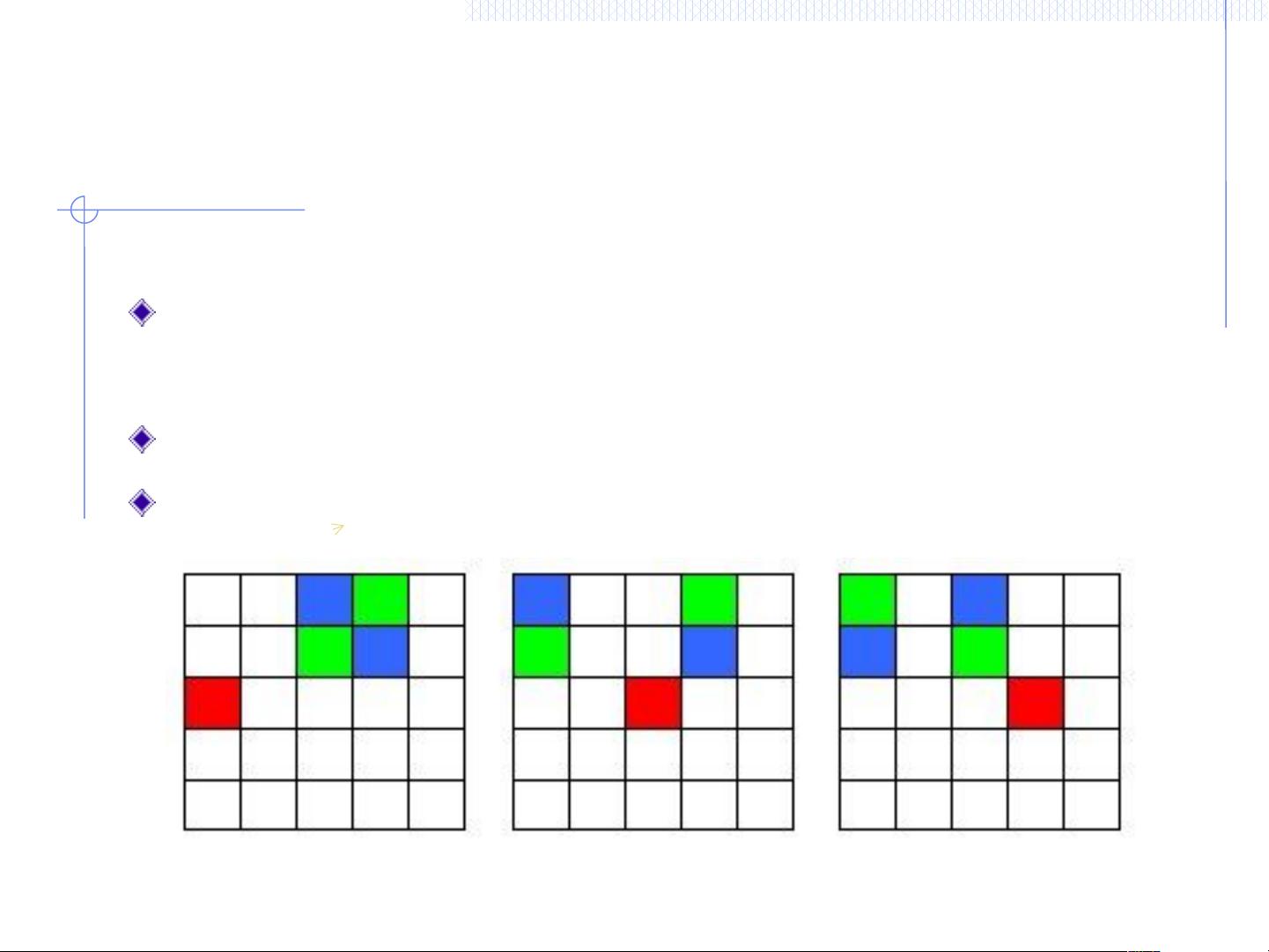 在提供的例子中，一个经典的动态规划问题是在n×n的棋盘上放置n个车，使得它们无法互相攻击。常规的解决方法是计算排列组合，但这里采用状态压缩的方法。每种放置状态可以用一个二进制数来表示，其中1表示该列有车，0表示没有。通过递推，我们可以计算出到达特定状态的放置方案数。 状态压缩的关键在于找出状态之间的转移规则。在这个问题中，每行只能放一个车，所以我们可以通过检查当前状态s的二进制表示来确定它是如何从上一行的状态转移过来的。例如，如果s的第i+1位为1，表示第i+1列有车，那么转移可能来自于之前两行的不同放置组合。通过这种方式，我们可以构建递推公式来计算每个状态的方案数。 状态压缩是一种高级的动态规划技巧，它需要对位运算有深入理解，并能够将复杂的状态表示简化。通过实例学习和练习，可以逐步掌握这种技巧，从而解决更复杂的问题。在实际编程中，尤其是在限制内存和时间的算法竞赛中，状态压缩往往能提供更优的解决方案。