迪杰斯特拉算法详解：城市交通最短路径探索

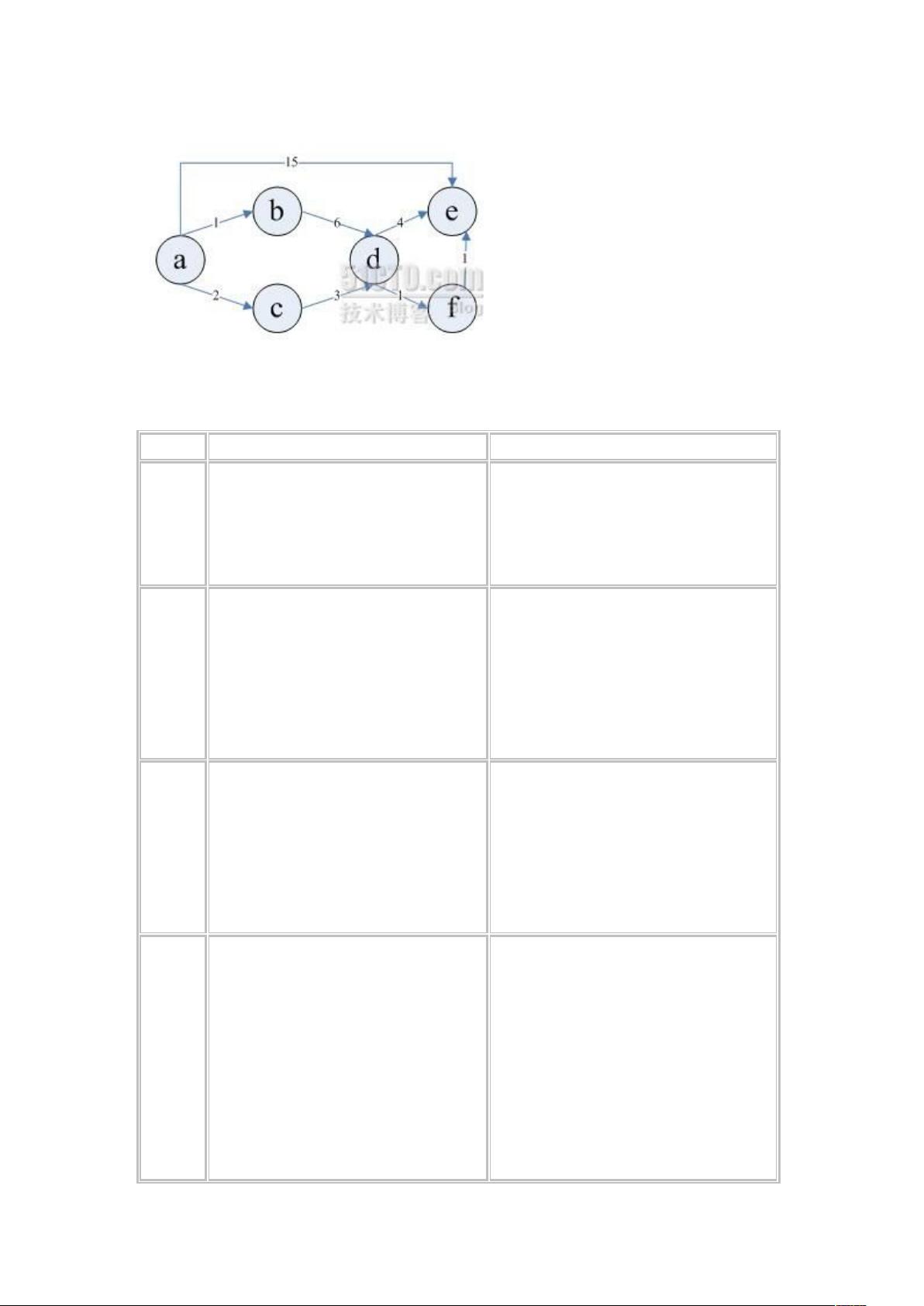
迪杰斯特拉算法是一种用于解决单源最短路径问题的高效搜索算法，它在图论中具有广泛应用，特别是在交通路线优化、网络路由等领域。本篇小结主要围绕该算法进行详细的总结和代码描述。 首先，问题背景设定在一个城市交通网络中，Kiki希望找到从她家到朋友家的最短路径，同时考虑到可能的换乘。这个问题可以转化为在一个有向图中寻找源点a到其他所有顶点的最短路径，图中包含若干个公交站，用数字1到n表示。 算法的步骤如下： 1. 初始化：选择起始点a加入集合S（已知最短路径集合），将所有其他节点（除a外）放入集合U（待处理节点集合）。开始时，a到自身是最短路径，值为0；a到其他节点（如b）的最短路径为已知距离。 2. 搜索过程：每次从U集合中选取一个距离源点a最近的节点，将其加入S。对于这个新加入的节点，更新其与源点之间的最短路径。例如，从a出发到b的最短路径由1变为1，因为通过a直接到达b比之前的间接路径更短。 3. 递归查找：对S集合中的每个节点，以它为中间点，检查与U集合中所有未访问节点的连接，更新最短路径。比如，从a到c再到d的路径，如果比已知路径更短，则更新路径信息。 4. 重复步骤2和3，直到U集合为空，或者无法再找到新的更短路径为止。在这个过程中，会不断更新源点到各个节点的最短路径。 5. 最终结果：当算法结束时，S集合包含了所有节点，其中的最短路径就是从a到所有其他节点的最小距离。 在给出的图例中，展示了算法的具体应用。通过逐次迭代，算法能够找出最优路径，如a->b->d的最短路径是7，a->c->d->f的最短路径是6，以此类推。迪杰斯特拉算法的关键优势在于它的局部最优策略，确保在每一步都选择当前状态下可达的最短路径，从而逐步接近全局最优解。 总结来说，迪杰斯特拉算法适用于静态图，对于边的权重是有界的，并且通常用于单源最短路径问题。掌握并理解这个算法，有助于我们在实际问题中寻找最优解决方案，尤其是在处理城市交通规划这类实时性要求较高的场景。