PCA算法解析：降维与数据标准化

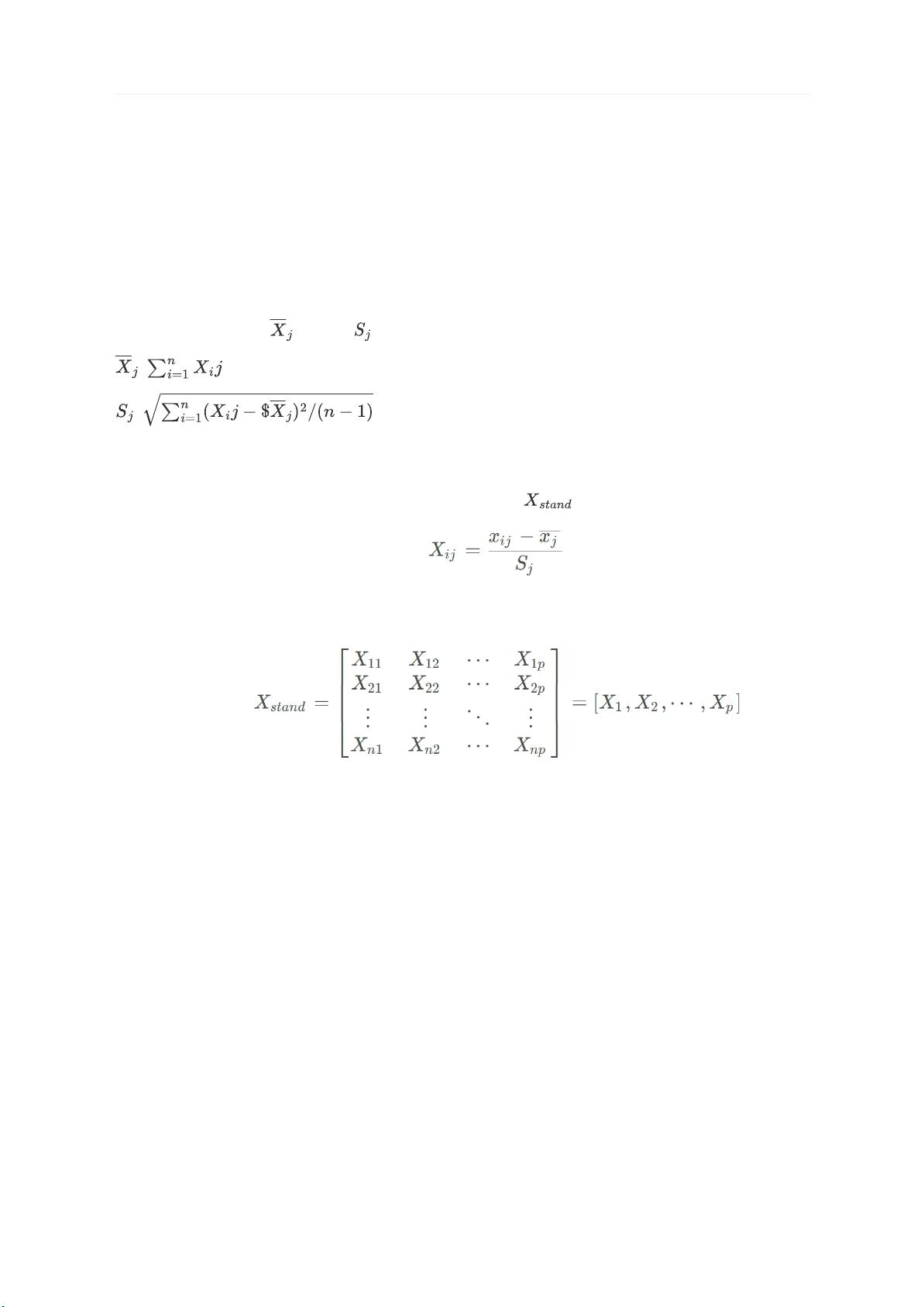
PCA（主成分分析）是一种常用的数据预处理方法，旨在通过线性变换将原始高维数据转化为一组线性无关的低维表示，同时保留原始数据的主要信息。PCA的主要目的是降低数据的复杂性，去除噪声，以及简化数据分析过程。在这个过程中，PCA会寻找数据中的主要变异方向，也就是主成分。 在PCA算法的步骤中： 1. 数据标准化：首先，对数据进行预处理，计算每个特征的均值和标准差，然后将数据标准化，使得每个特征的均值为0，标准差为1。这样可以消除不同特征之间的量纲差异，确保所有特征在同一尺度上。 2. 标准化特征矩阵：将每个样本的特征进行标准化，得到一个标准化特征矩阵。这个矩阵中的每个元素都是原始数据减去其所在列的均值，然后除以该列的标准差。 3. 计算协方差矩阵：协方差矩阵用于度量特征之间的相关性。矩阵中的每个元素表示两个特征之间的协方差，反映了它们的变异程度和方向。 4. 计算贡献率和累计贡献率：特征值代表了主成分解释原始数据变异的程度，贡献率是每个主成分的方差占总方差的比例。累计贡献率则是前n个主成分的贡献率之和，通常选取累计贡献率达到一定阈值（如85%）的主成分作为新的数据表示。 5. 选取主成分：根据累计贡献率选择重要的主成分。例如，如果累计贡献率达到85%，那么可以选择前n个主成分，这n个主成分可以捕获原始数据的大部分信息。 在给定的代码中，使用了Python的数据科学库，如pandas、numpy、scipy和matplotlib等，来实现PCA的计算。首先读取鸢尾花数据集，然后进行数据标准化，计算协方差矩阵，接着求解协方差矩阵的特征值和特征向量。最后，计算贡献率和累计贡献率，并确定需要保留的主成分数量。 特征值和特征向量的排序很重要，因为它们决定了主成分的顺序。较大的特征值对应着更重要的主成分。通过选取累计贡献率大于85%的主成分，可以保证新数据表示的效率和信息保留程度。在实际应用中，PCA不仅用于数据可视化（如二维或三维图），还常用于机器学习模型的特征选择和降维。