利用SRS效应的高效稀土掺杂光纤放大器研究
189 浏览量
更新于2024-08-27
收藏 703KB PDF 举报
本文主要探讨了"高效非线性光纤放大器"(Nonlinear Fiber Amplifier, NFA)在克服常规光纤激光器功率提升过程中面临的挑战——受激拉曼散射(SRS)效应。SRS是限制光纤激光器功率增益的一个重要因素，因为它可能导致能量在泵浦光波长附近自发地转移到其他波长，从而降低整体效率。传统方法倾向于抑制SRS，但NFA则是一种创新策略，通过巧妙利用SRS的特性来实现功率的高效放大。
NFA主要研究在掺稀土元素的光纤中如何控制和利用SRS过程，这种光纤因其独特的光学特性，能够有效地管理SRS带来的影响。作者在文章《HighPowerLaserScienceandEngineering》(2018年卷6, 第51期, 11页)中提出了一个全面的理论模型，该模型旨在理解和优化NFA的设计参数，如光纤材料的选择、泵浦光源的特性以及信号波长的调控，以实现高功率输出且保持低噪声水平。
文章的结构可能包括以下几个关键部分：
1. 引言：阐述SRS问题在光纤激光器中的重要性和传统解决方案的局限性。
2. 非线性纤维放大器原理：解释NFA的工作原理，如何通过选择性地增强有益的SRS过程而抑制有害的。
3. 理论模型：详细介绍提出的模型，包括数学描述、参数分析和仿真结果，以展示NFA如何在理论上克服SRS障碍。
4. 设计与实现：讨论实验设计，包括光纤制造、泵浦源选择和系统集成的关键步骤。
5. 实验结果与分析：展示实际操作中NFA的性能提升，包括功率增益、噪声特性以及可能的优化方向。
6. 结论与前景：总结研究成果，并展望NFA在未来高功率光纤激光器发展中的潜力和可能的应用领域，如工业加工、通信系统和科学研究。
这篇文章对高功率光纤激光技术的进步具有重要意义，它不仅提供了新的思考角度，也为解决传统技术难题提供了创新性的解决方案。由于是开放获取的文章，其研究方法和成果可以广泛应用于学术界和工业界，推动相关技术的发展和商业化应用。
Toward high-power nonlinear fiber amplifier 3
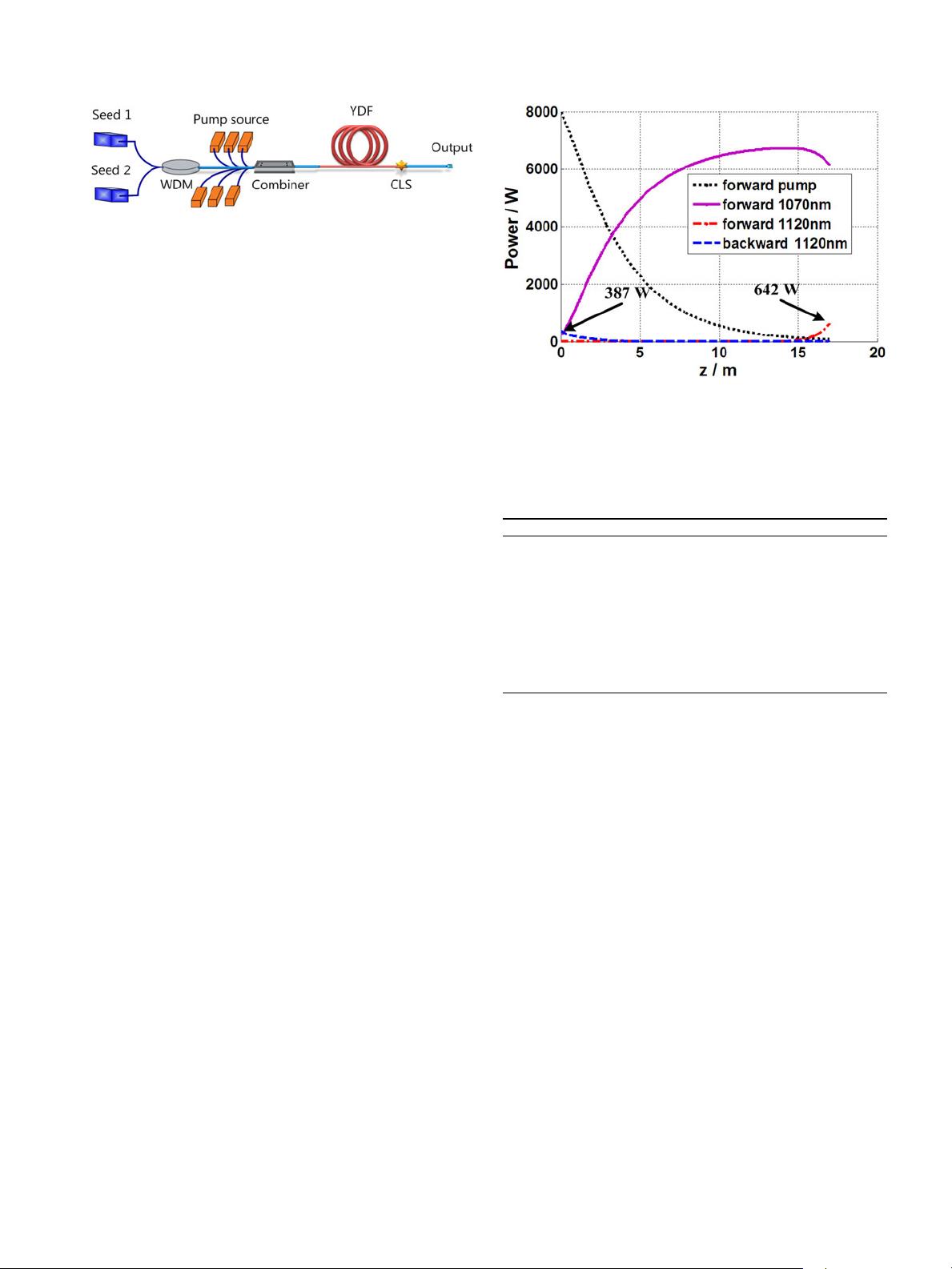
Figure 1. The basic system setup of the NFA.
The emission spectrum of Yb-doped fiber (from 970 nm
to 1200 nm) can be divided into discrete spectral channels
with width of 1λ. The subscript k represents the kth channel
but p, s
1
and s
2
represent the pump and two signal waves
specially. The superscript ± corresponds to positive and
negative directions, respectively. N (z) is the Yb ions concen-
tration distribution along the fiber, for passive fiber N (z) =
0; N
2
(z) is the excited state population; P
si
represents the
signal power; P(z, λ
k
) is the power of laser λ
k
; σ
a
and σ
e
are
Yb absorption and emission cross sections, respectively
[41]
.
Γ is the overlapping factor between the pump (ASE signal)
and the fiber doped area. g
R
is the Raman gain coeffi-
cient; α is the loss coefficient. 2hv1v is the Raman noise
and the factor 2 corresponds to two polarization states. h
is the Planck constant; v is frequency; 1v is bandwidth
of the signal. For spontaneous Raman noise we assume
the bandwidth equals the gain bandwidth that is about
40 THz.
The boundary conditions can be described by the follow-
ing equations:
P
+
(0, λ
k,si
) = R
1
(λ
k,si
)P
−
(0, λ
k,si
) + P
+
0
(λ
k,si
), (6)
P
−
(L , λ
k,si
) = R
2
(λ
k,si
)P
+
(L , λ
k,si
) + P
−
0
(λ
k,si
), (7)
where R
1
and R
2
refer to the reflectivity in the left and
right side, respectively. Then this model can be numerically
calculated by the finite-difference method
[42]
.
3. Numerical analysis of nonlinear fiber amplifier
3.1. Power scaling potential of NFA
SRS is a main restriction for the power scaling of wide band-
width YDFA. There is still not a straightforward technique
that can suppress SRS effectively without introducing any
drawback in YDFA. In this section we would like to show
the advantage of the NFA in the potential of suppressing
SRS by using a numerical example. The parameters used
in the calculation are shown in Table 1. It is a co-pumping
scheme with power of 8000 W. The gain fiber is 20/400 µm
(core/inner diameter) double cladding YDF.
Firstly, we calculate a traditional case of only the 1070 nm
laser in the seed. The seed power is 200 W. The power
distribution along the fiber is shown in Figure 2. It can be
found in this case that the signal power can reach more
Figure 2. The power distribution of pump, signal, and Raman waves in
forward and backward propagating directions. It can be found that Raman
Stokes wave (1120 nm) has arisen in both directions, and the power is
642 W and 387 W for forward and backward directions, respectively.
Table 1. The parameters of the calculated fiber amplifier.
Parameter Value Unit Parameter Value Unit
λ
p
976 nm λ
s1
1070 nm
λ
s2
1120 nm λ
s3
1180 nm
d
core
20 µm d
inner-clad
400 µm
P
p
8000 W τ 0.84 ms
P
+
0
(s1) 200 W Γ
k
0.8 —
L 17 m α 2 × 10
−3
m
−1
1v
1
0.3 THz 1v
2
0.3 THz
1v
3
40 THz N
0
4.33 × 10
25
m
−3
g
R
0.5 × 10
−13
m/W g
R1
0.48 × 10
−13
m/W
than 6000 W if other nonlinear effects or thermal effects are
ignored. However, such a system is unpractical for Raman
Stokes wave (1120 nm) that can be found in both directions.
Especially in the backward direction, the power of 1120 nm
laser in the fiber core is about 387 W, which is a big hidden
danger for the high-power laser system. From this point of
view, SRS is a limitation of the traditional Yb-doped fiber
amplifier system. For comparison, we would like to give
an example with similar condition for the NFA. The only
change is that a 10 W 1120 nm laser is added in the seed. The
1120 nm laser corresponds to the first-order Stokes wave of
1070 nm laser. The other parameters of the amplifier are the
same as that shown in Table 1.
Figure 3 is the calculated results of the NFA. In this am-
plifier, the 1070 nm laser is firstly amplified by the ytterbium
gain, and as the 1120 nm laser propagates in the fiber core,
it reaches the Raman threshold and begins to dominate the
following amplification
[34]
. Finally, the power of 1070 nm
laser is all transferred to the Stokes wave (1120 nm) at the
output end. It can be found in Figure 3(b) that the sum of the
laser power of 1070 nm and 1180 nm is less than 5 W. At the
backward output end, seen in Figure 3(c), the total output
剩余10页未读，继续阅读
2020-03-03 上传
2022-03-16 上传
2021-01-27 上传
2021-02-21 上传
2021-02-11 上传
2021-01-26 上传
2024-03-31 上传
2011-03-23 上传
2021-02-07 上传
2021-02-21 上传
weixin_38559727
- 粉丝: 6
- 资源: 924
我的内容管理
展开
最新资源
- 深入浅出：自定义 Grunt 任务的实践指南
- 网络物理突变工具的多点路径规划实现与分析
- multifeed: 实现多作者间的超核心共享与同步技术
- C++商品交易系统实习项目详细要求
- macOS系统Python模块whl包安装教程
- 掌握fullstackJS：构建React框架与快速开发应用
- React-Purify: 实现React组件纯净方法的工具介绍
- deck.js：构建现代HTML演示的JavaScript库
- nunn：现代C++17实现的机器学习库开源项目
- Python安装包 Acquisition-4.12-cp35-cp35m-win_amd64.whl.zip 使用说明
- Amaranthus-tuberculatus基因组分析脚本集
- Ubuntu 12.04下Realtek RTL8821AE驱动的向后移植指南
- 掌握Jest环境下的最新jsdom功能
- CAGI Toolkit：开源Asterisk PBX的AGI应用开发
- MyDropDemo: 体验QGraphicsView的拖放功能
- 远程FPGA平台上的Quartus II17.1 LCD色块闪烁现象解析
