字典树与KMP算法详解教程

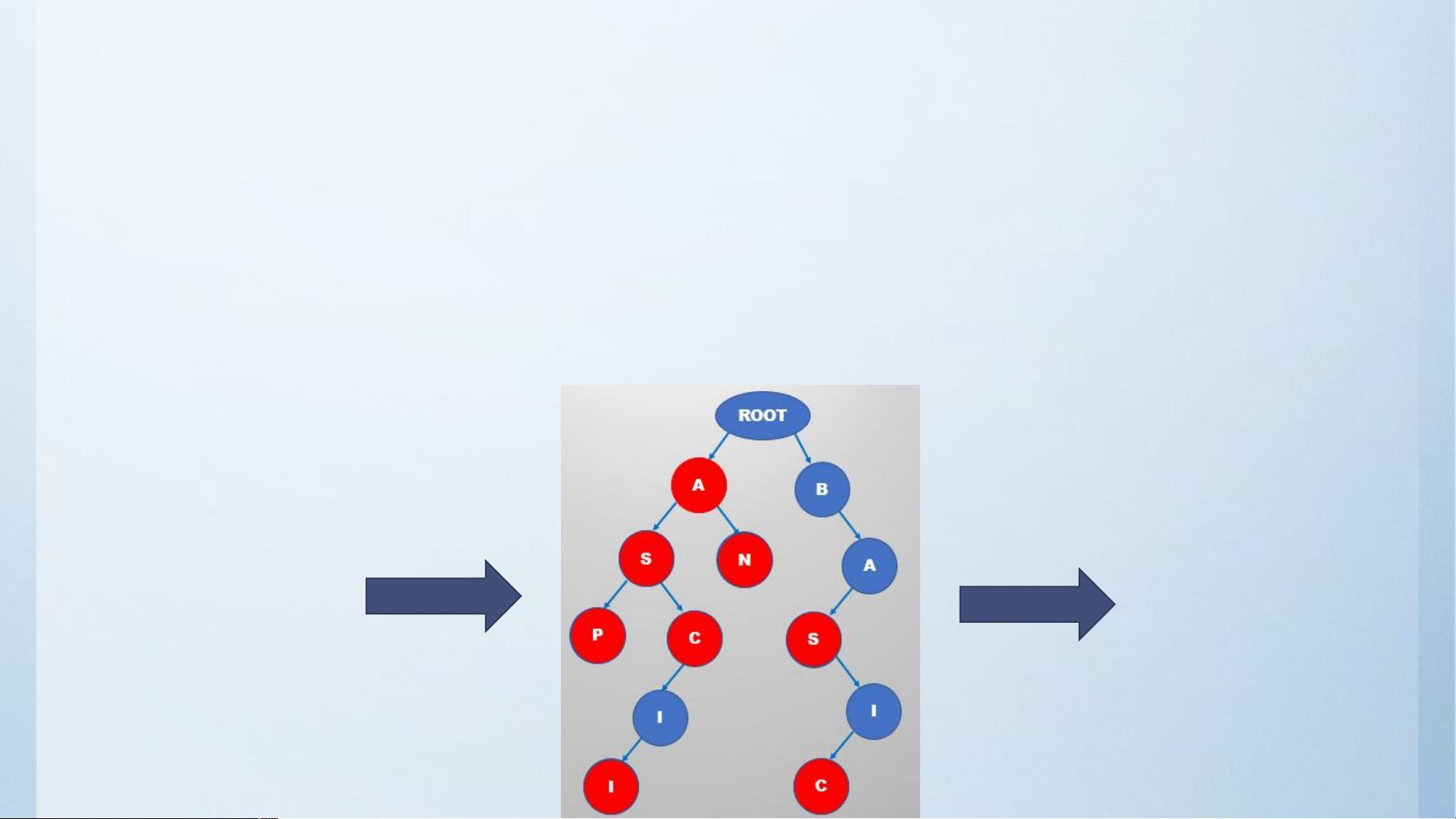
KMP算法详细教学教程 在这个教程中，我们将深入探讨著名的Knuth-Morris-Pratt (KMP) 算法，这是一种高效的字符串匹配算法，常用于在文本中查找特定子串。KMP算法的核心在于避免回溯过程，通过预处理模式串，构建部分匹配表（也称失配函数或失败跳转函数），使得在匹配过程中遇到不匹配的情况时，可以直接根据表中的信息跳过部分字符，减少不必要的比较。 首先，我们会介绍字典树（Trie或前缀树）的基础概念，它是数据结构的一种，用于高效存储和查找字符串。字典树利用字符串的公共前缀特性，存储大量字符串时能节省空间。构建字典树时，每个节点代表一个字符，从根节点到叶子节点的路径表示一个完整的单词。通过优化查找操作，字典树支持快速检索，比如在查找是否一个单词可以由其他单词拼接时，字典树的效率远高于朴素的逐个字符对比方法。 KMP算法与字典树相辅相成，字典树可以用来辅助构建部分匹配表。在KMP算法中，部分匹配表记录了模式串中每个位置在不匹配时可能需要跳过的最大字符数量。这样，在匹配过程中，当遇到不匹配时，算法可以根据表中的值决定前进多少步，而不是立即回溯，从而大大减少了比较次数。 在实现KMP算法时，我们会看到以下关键步骤： 1. **模式串的预处理**：创建部分匹配表，计算出模式串中每个位置的失配值，即最长的不包含字符的前缀，使得该前缀之后的字符仍能匹配。 2. **匹配过程**：在目标串中查找模式串，每当遇到不匹配时，利用部分匹配表中的信息更新当前匹配的位置，而不是直接回溯。 3. **代码实现**：通常使用数组或类似的数据结构来存储部分匹配表，并结合循环结构实现查找过程，避免重复计算和无效比较。 KMP算法因其时间复杂度为O(n + m)，其中n是目标串的长度，m是模式串的长度（最优情况下），相比于简单的线性搜索有显著的优势，特别是在大规模数据处理中。掌握KMP算法及其与字典树的结合使用，将有助于提高程序性能，尤其是在文本处理和字符串匹配应用场景中。