线性回归模型：异方差性与估计问题

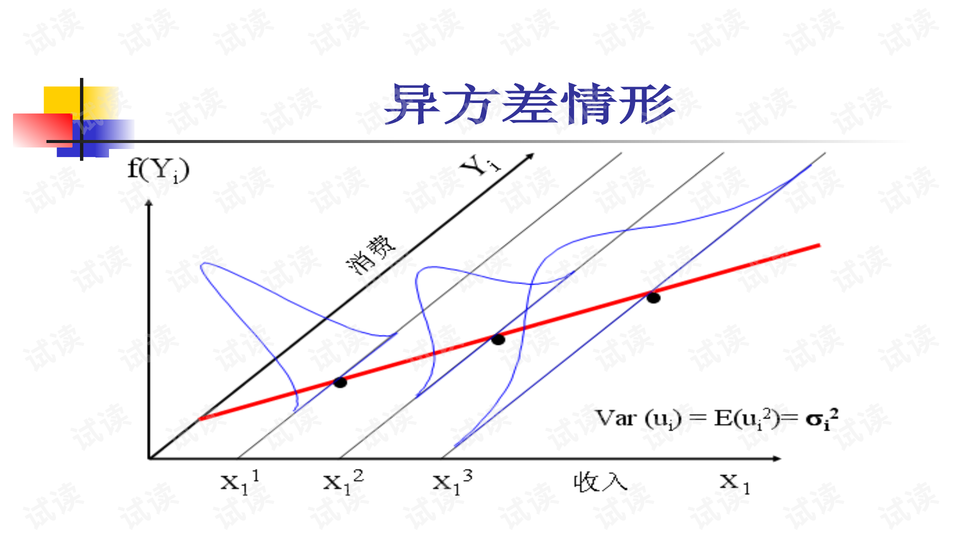
"异方差情形-线性回归模型" 线性回归模型是统计学中常用的一种数据分析工具，用于预测连续变量的值。简单线性回归模型是最基础的形式，它包含一个自变量 \( x \) 和一个因变量 \( y \)，可以表示为 \( y = \beta_0 + \beta_1 x + u \)，其中 \( \beta_0 \) 是截距项，\( \beta_1 \) 是斜率，\( u \) 是误差项或随机扰动项。 在简单线性回归中，有几个重要的假定： 1. 线性于参数：模型中的关系是线性的，即 \( y \) 与 \( x \) 的关系可以用一条直线来描述。 2. 随机抽样：样本是从总体中随机抽取的，确保样本的代表性。 3. 解释变量的样本有变异性：自变量 \( x \) 在样本中存在变异，不是完全相同。 4. 零条件均值：误差项 \( u \) 对于任何给定的 \( x \) 值，期望值为0，即 \( E(u|x) = E(u) = 0 \)。 5. 同方差性：误差项 \( u \) 的方差是常数，不随 \( x \) 的变化而变化，记作 \( Var(u|x) = \sigma^2 \)。 在同方差性假设下，最小二乘法(Ordinary Least Squares, OLS)可以用来估计模型参数。通过最小化残差平方和（RSS）来找到最佳的 \( \beta_0 \) 和 \( \beta_1 \) 的估计值 \( \hat{\beta}_0 \) 和 \( \hat{\beta}_1 \)。拟合的直线方程可以表示为 \( \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x \)，其中 \( \hat{y} \) 是预测值。 拟合优度（R-squared, \( R^2 \)）是衡量模型解释变量变异能力的指标，它是解释平方和（SSE）占总平方和（SST）的比例。\( R^2 \) 越接近1，模型对数据的解释能力越强；反之，如果 \( R^2 \) 接近0，表示模型对数据的解释能力较弱。 当面临异方差性（即误差项的方差不是常数，而是随 \( x \) 的变化而变化）时，线性回归的估计会出现问题。异方差性可能导致OLS估计的参数不具有最佳线性无偏估计(BLUE)性质，并影响到区间估计和假设检验的准确性。为了纠正异方差性，可以采用加权最小二乘法（Weighted Least Squares, WLS），根据误差项方差的变化情况赋予观测点不同的权重。 另外，误差项的概率分布对线性回归分析的其他方面至关重要。在经典线性回归假定中，误差项通常被假定为正态分布，具有零均值和相同的方差。如果这个假设成立，那么OLS估计量具有最优性质，如无偏性和最小方差性。但实际应用中，正态性假设可能难以满足，因此可能需要通过残差图或其他统计测试来检查并处理非正态性问题。 理解线性回归模型的基本假设，包括同方差性、误差项的正态分布等，对于正确解读模型结果和进行有效的预测至关重要。在遇到异方差性时，应考虑调整模型或采用适当的修正方法来提高模型的稳健性。