Bresenham算法详解：高效绘制直线

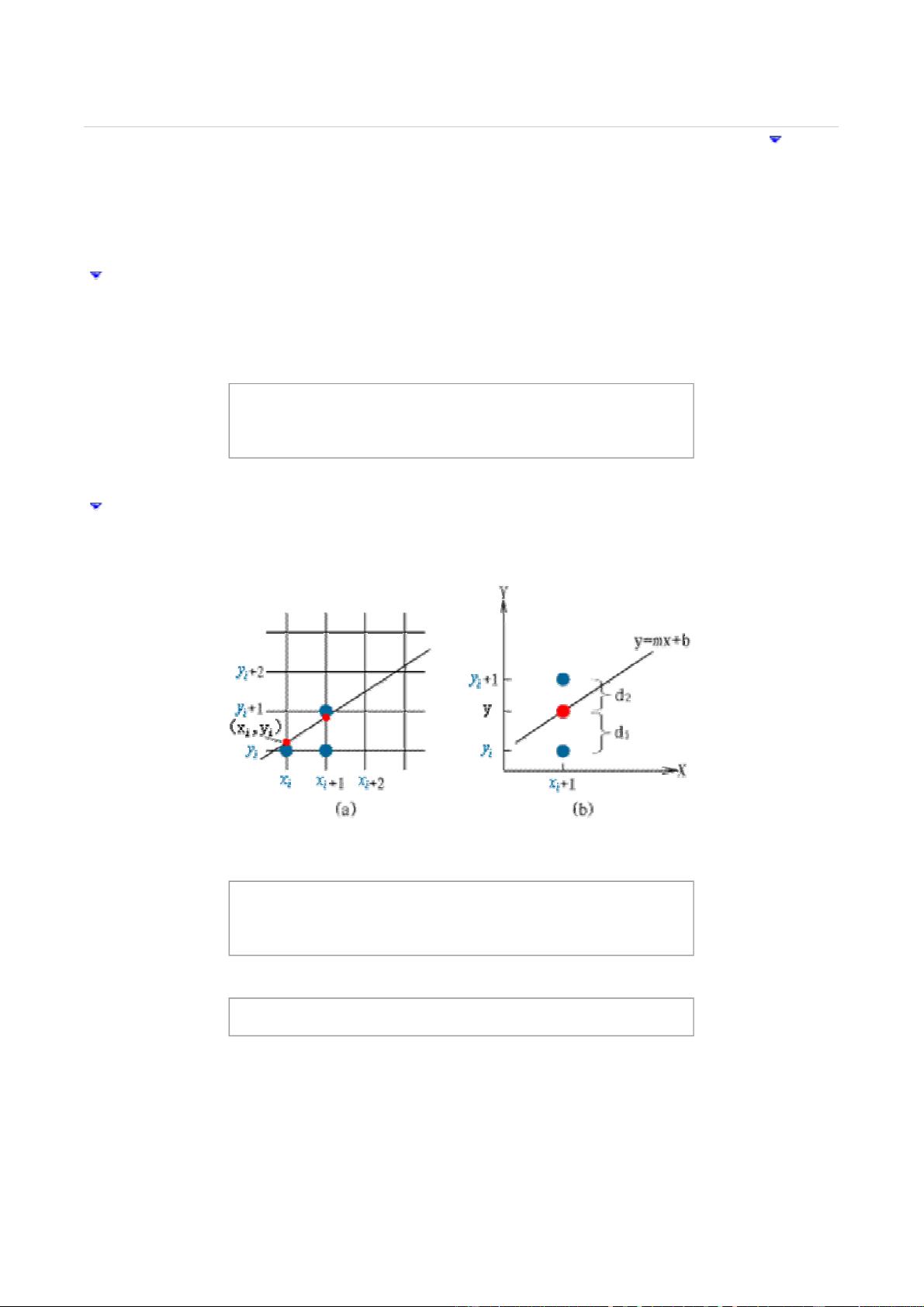
"Bresenham算法是一种在计算机图形学中用于绘制离散点构成的直线的高效算法，尤其适用于像素级别的图像处理。该算法由John E. Bresenham在1965年提出，主要针对像素化的显示系统设计，以避免浮点运算，提高绘制速度。" 在二维图形生成中，Bresenham算法是解决从(x1, y1)到(x2, y2)直线渲染问题的关键方法。相比于DDA（Digital Differential Analyzer）算法，Bresenham算法避免了循环中的浮点数运算，从而显著提高了效率。DDA算法通过连续计算每个像素点的坐标，而Bresenham算法则利用误差累积的方式来确定应该画哪些像素。 Bresenham算法的核心思想是在每一步迭代中，基于当前像素点的坐标(x, y)和误差项E来决定下一个像素点的位置。对于斜率0≤m≤1的情况（即y轴的变化小于等于x轴的变化），我们可以假设当前像素点(xi, yi)是直线的最佳近似，然后通过比较误差项E来确定下一个像素点是(xi+1, yi)还是(xi+1, yi+1)。 误差项E的计算公式为： E = 2m(xi+1) - 2yi + 2b - 1 这里，m代表直线的斜率，b是常数项。E的符号决定了像素点的选择： 1. 当E > 0时，选择(xi+1, yi+1)作为下一个像素点，因为此时理论上的直线点更接近这个位置。 2. 当E ≤ 0时，选择(xi+1, yi)作为下一个像素点，因为直线点更接近这个位置。 3. 当E = 0时，两个像素点距离相等，算法通常会选择(xi+1, yi+1)，以保持直线的一致性。 在实际实现中，Bresenham算法通常用位操作来进一步优化，减少计算量，提高性能。此外，对于斜率大于1的情况，可以通过坐标变换将其转换为0≤m≤1的情况，然后再应用算法。 总结来说，Bresenham算法是一种高效且广泛应用于计算机图形学的直线绘制算法，通过避免浮点运算，它能够快速地在像素级别生成直线，是计算机图形界面和图像处理软件不可或缺的一部分。