优化存储：程序员视角下的特殊矩阵压缩方法

在计算机科学中，特殊矩阵的压缩存储是一种优化数据结构技术，特别是在处理大量稀疏矩阵时，如对称矩阵。这种存储方式对于节省内存空间至关重要，尤其是在矩阵中包含大量零元素时。本文主要关注于如何针对特定矩阵类型进行高效的存储设计。 首先，理解数组大小的计算是关键。在编程中，如果要对称矩阵进行压缩存储，通常需要考虑矩阵的行数（R）和列数（C），因为对称矩阵的上三角或下三角部分只需要存储一半的元素。如果矩阵是完全对称的，即是对角对称（比如正定矩阵），则实际上只需要存储下三角或上三角的一半。所以，对于一个R×C的对称矩阵，如果采用压缩存储，数组大小应为R*(C/2)。 站在程序员的角度，对称矩阵的压缩存储通常涉及创建一个一维数组来表示矩阵，这样可以避免存储重复的元素。例如，对于一个对角线以上的元素，可以通过一个索引i进行访问，通过公式`index = i * (i + 1) / 2 + (j - i)`（对于下三角，对于上三角取相反的索引）来确定实际的二维数组位置。同时，可以实现一个映射函数，将矩阵元素的逻辑坐标（i, j）转换为一维数组的索引，以便快速访问和修改数据。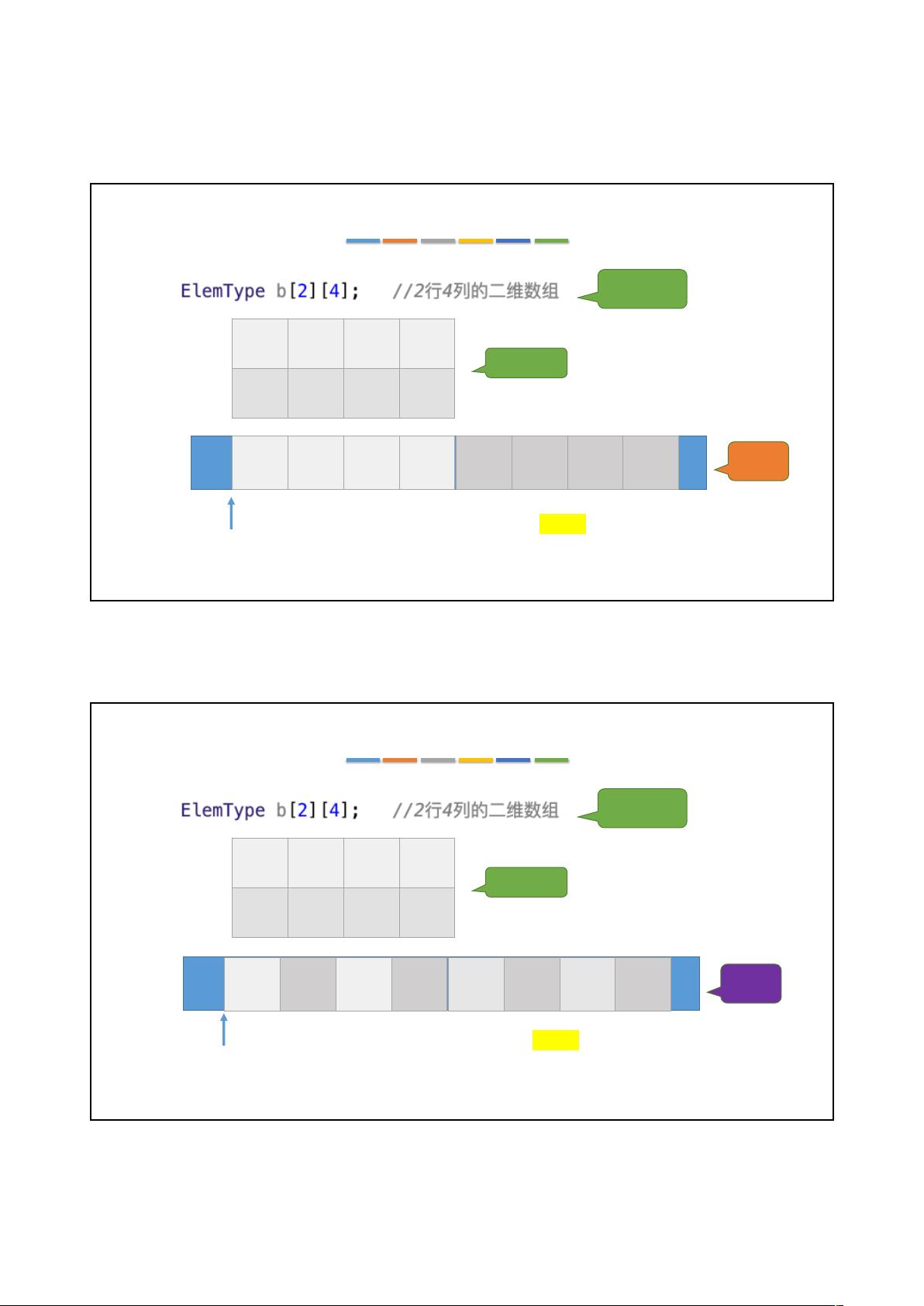 一维数组和二维数组的存储结构是基础，对于一维数组，元素物理上是连续存放的，通过数组下标计算实际地址。二维数组有行优先和列优先两种存储方式。行优先存储时，数组元素按行顺序排列，每个元素的地址计算公式是`LOC + (i * N + j) * sizeof(ElemType)`，其中LOC是数组起始地址，N是列数。而列优先存储则是将每列元素放在一起，索引计算略有不同。 在处理二维数组时，特别需要注意的是稀疏矩阵的存储优化，因为它并非每个位置都有非零值。对于二维数组的压缩存储，程序员需要考虑矩阵的稀疏特性，可能使用稀疏矩阵库或者自定义的数据结构，如压缩行存储（Compressed Row Storage, CRS）或压缩列存储（Compressed Column Storage, CCS），这些方法能够减少存储空间的需求。 总结来说，特殊矩阵的压缩存储是一个重要的数据结构优化技术，通过合理的算法和数据结构设计，可以极大地提高存储效率，尤其是在处理大量稀疏矩阵时。对于程序员来说，理解矩阵的性质、选择合适的存储方式，并编写映射函数以高效地操作和访问这些数据，是提高代码性能的关键。