双线性插值算法详解与实现

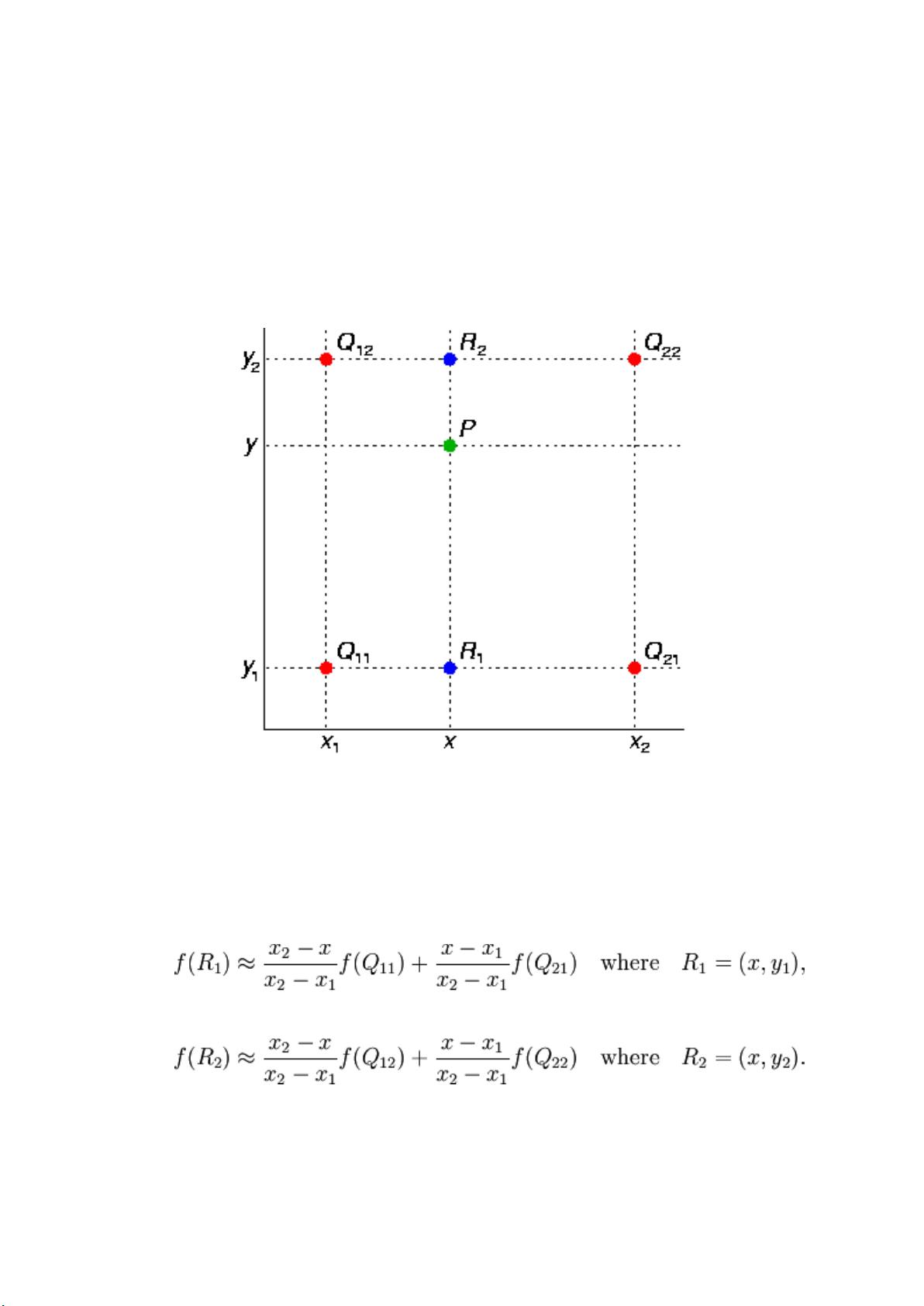
"双线性插值算法用于图像缩放，是一种在二维空间中进行插值的方法，通过在两个方向上分别进行线性插值来计算新像素的值。这种算法在位图处理中广泛使用，可以提高放大图像的质量，避免像素不连续的问题，但同时也可能导致图像细节的损失和轮廓模糊。" 双线性插值算法的核心在于对目标图像中的每个新像素位置，找到源图像中最近的四个像素（Q11, Q12, Q21, Q22），然后基于这些像素的位置关系，使用加权平均来计算新像素的值。新像素的创建遵循两个步骤：首先进行X方向的线性插值，然后进行Y方向的线性插值。 在X方向的线性插值中，计算新像素的红色分量（其他颜色通道类似）可由以下公式表示： δR2 = ColorQ22 - ColorQ12 * ∆col + ColorQ12 * 256 (1) δR1 = ColorQ21 - ColorQ11 * ∆col + ColorQ11 * 256 (2) 其中，∆col是目标像素相对于源图像像素区域左上角的水平距离，ColorQ(X)表示像素Q(X)的颜色。这里的计算涉及到像素位置的浮点运算，为了确保精度，通常会将整数部分左移8位，然后与255进行与操作，以获取实际的像素距离。 完成X方向的插值后，进行Y方向的线性插值，公式如下： ColorP = δR2 * 256 + δR2 - δR1 * ∆row >> 16 (3) 这里的∆row是目标像素相对于像素区域左上角的垂直距离，同样需要进行类似的处理。最后的结果需要右移16位以恢复正确的颜色值。 算法的执行流程如下： 1. 对目标图像的每一行进行迭代。 2. 根据目标像素的位置找到源图像中对应的4个像素。 3. 计算X方向的线性插值，得到δR1和δR2，并保存δR1。 4. 在下一行中，δR2将变为当前行的δR1。 5. 使用X方向的结果，进行Y方向的线性插值，得到最终的新像素颜色值ColorP。 6. 将ColorP赋值给目标图像的当前像素。 虽然双线性插值可以提供较好的图像放大效果，但其低通滤波的特性意味着它会减少高频细节，可能导致图像变得稍微模糊。对于需要保留原始图像细节的应用，可能需要考虑使用更高级的插值技术，如三线性插值或最近邻插值。