最优线性滤波：维纳滤波与卡尔曼滤波解析

"2017现代数字信号处理第6章课件——东南大学杨绿溪教授讲解最优线性滤波，包括FIR和IIR维纳滤波以及离散卡尔曼滤波" 本章主要介绍了最优线性滤波技术，特别是维纳滤波和卡尔曼滤波在数字信号处理中的应用。首先，我们关注的是FIR（有限 impulse response）维纳滤波器。FIR维纳滤波是一种线性滤波器，设计目标是使信号在经过滤波后的均方误差最小化。这种滤波器可以应用于噪声抑制、线性预测和反卷积等多个领域，其中FIR维纳反卷积在MMSE（最小均方误差）均衡器中得到应用。此外，FIR维纳滤波器可以通过格型结构来实现，这有助于简化滤波器的设计和实现。 接着，课程探讨了IIR（无限 impulse response）维纳滤波器。IIR维纳滤波器分为非因果和因果两类。非因果IIR滤波器在平滑处理中发挥作用，而因果IIR滤波器则广泛用于滤波和预测问题。因果维纳滤波器在实际应用中尤其重要，因为它仅依赖于过去的输入信号来生成当前的输出，符合实时处理的要求。 除了FIR和IIR滤波器，课程还涉及离散卡尔曼滤波器。离散卡尔曼滤波是一种在线的、递归的最优估计方法，适用于处理随机过程的动态系统。在系统模型已知的情况下，卡尔曼滤波器能有效地估计出系统的状态，即使在存在噪声的情况下也能提供最佳线性估计。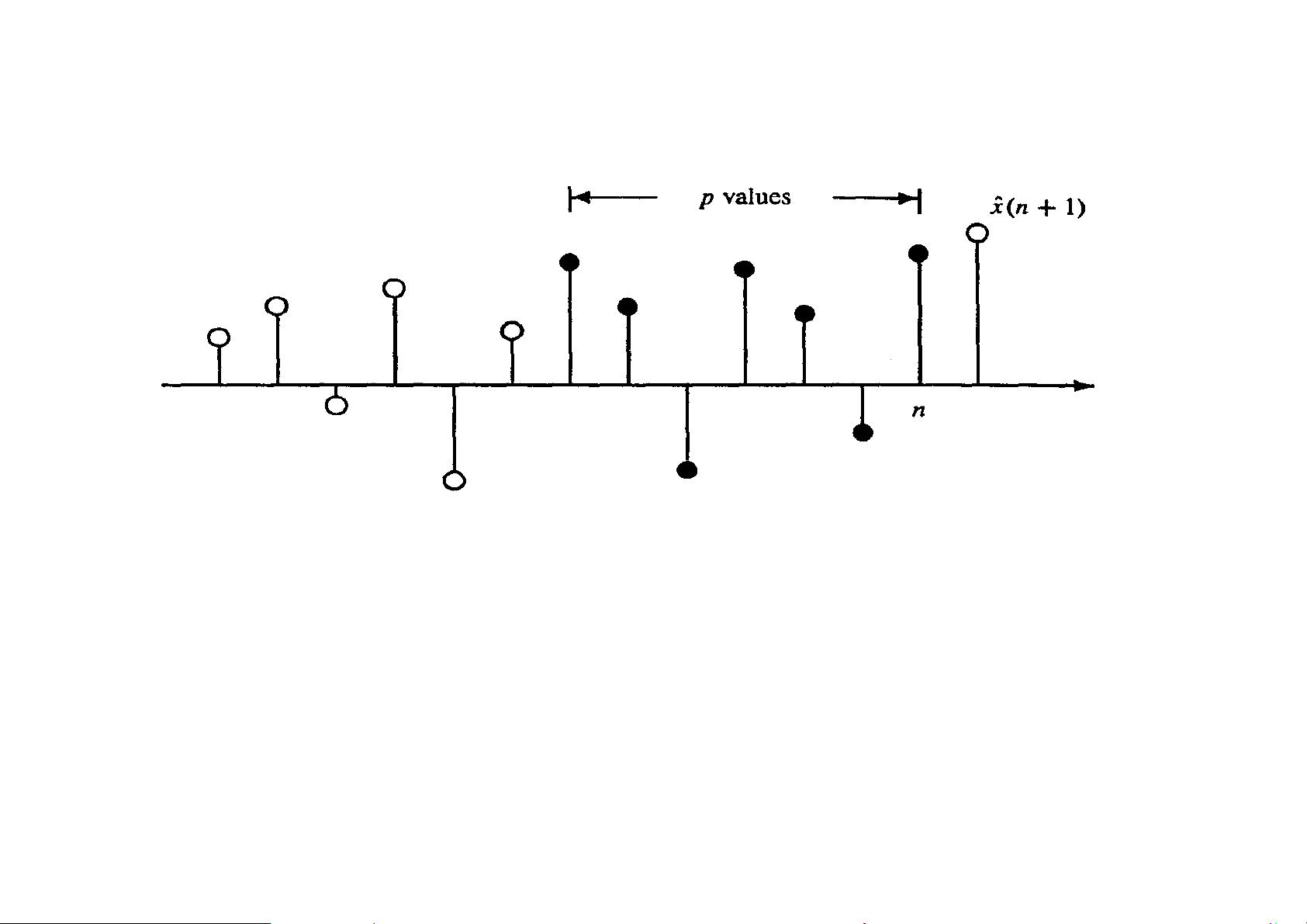 在信号处理的四个基本问题中，维纳滤波框架覆盖了滤波、平滑、预测和反卷积。滤波是通过当前和过去的数据估计当前信号；平滑允许使用未来的数据，通常用于非因果滤波器；预测是利用过去的数据来估计未来的信号，常用于线性预测器；反卷积则是用来消除信号经过其他滤波器后的失真。 这章内容深入浅出地讲解了最优线性滤波的基本理论和应用，对于理解和掌握数字信号处理中的噪声抑制、信号恢复和预测等关键问题具有重要意义。无论是FIR还是IIR维纳滤波，或是离散卡尔曼滤波，都强调了在噪声环境下的最优信号估计，是现代通信、图像处理、控制系统等领域不可或缺的工具。