根轨迹法分析线性控制系统：从定义到应用

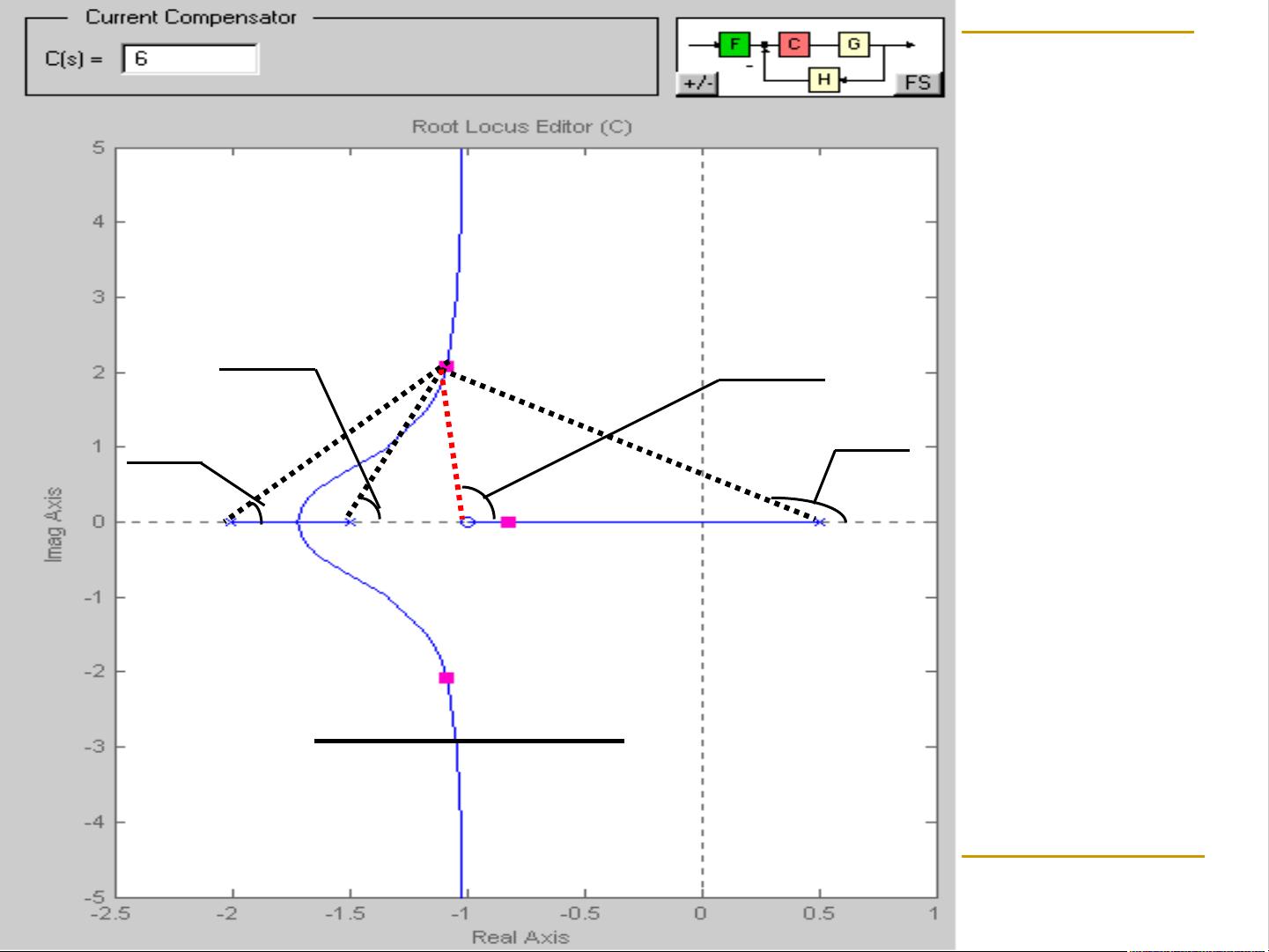
"自动控制理论：第四章 线性系统的根轨迹.ppt" 自动控制理论中的根轨迹方法是分析线性系统动态性能的一种重要工具，由依万斯（W.R.Evans）提出。根轨迹是通过绘制闭环系统特征方程的根随开环系统参数变化的轨迹，帮助我们理解系统稳定性、暂态响应和调节时间等关键性能指标的变化规律。 根轨迹的基本概念始于开环传递函数G(s)和H(s)，它们的乘积等于-1时，对应的s值就是闭环系统的特征方程的根。对于一个线性系统，其闭环传递函数为： 1 ) ( ) ( 1 s s K G H   =0 其中，K是系统增益，G(s)和H(s)分别是开环传递函数，s是复频变量。当K或系统结构中的其他参数改变时，特征方程的根也会随之变化，形成根轨迹。 以二阶系统为例，开环传递函数为： ) ( ) ( 1 a s s K G   具有两个开环极点0和-a。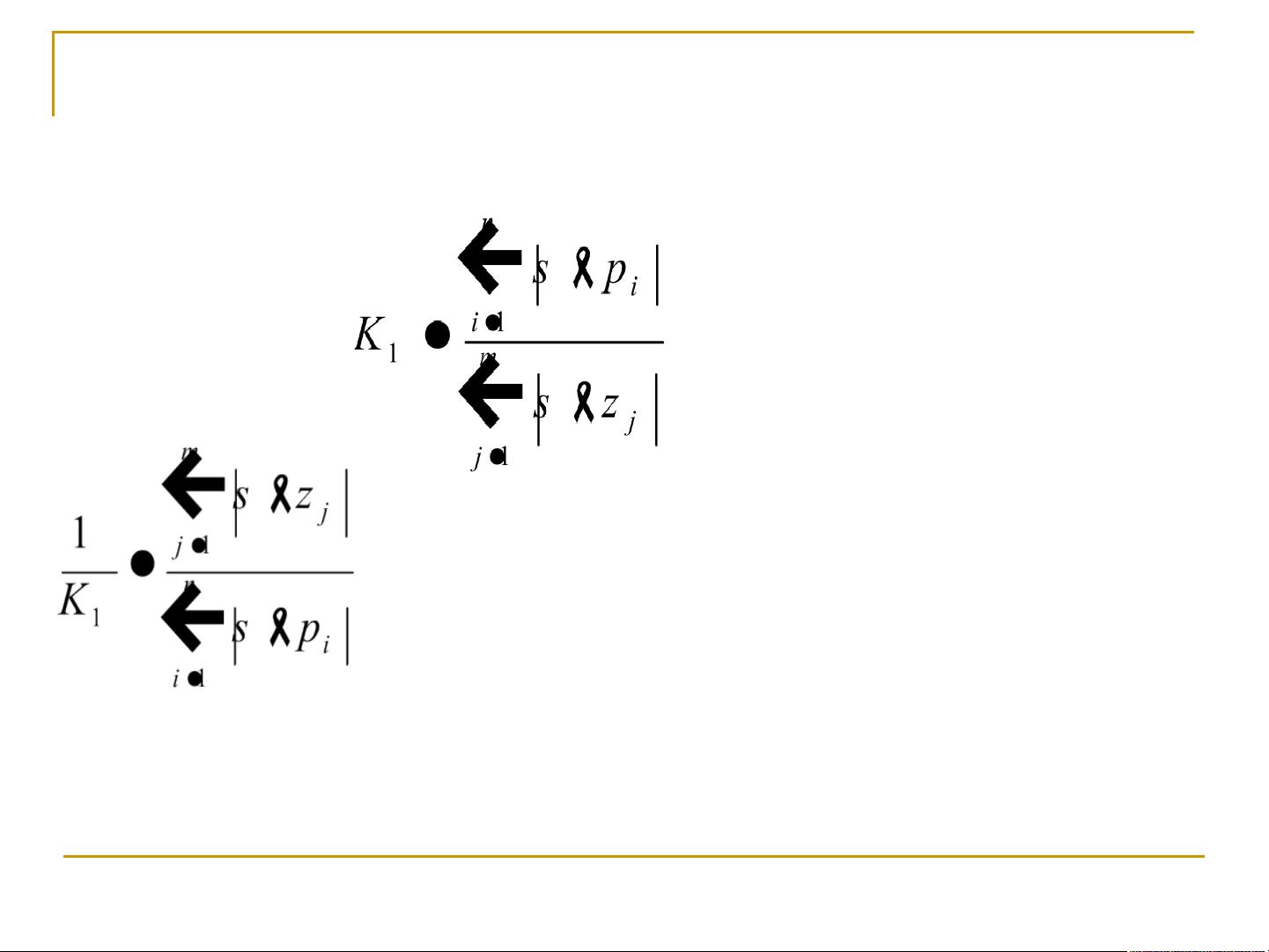当K变化时，闭环特征方程为： 0 1 2    K as s 根轨迹的绘制基于两个主要条件：幅值条件和相角条件。幅值条件指出，根轨迹上的点满足： 1 ) ( ) (  s H s G =1 相角条件则表示： 180 ) ( ) (  " ， 这两个条件确保了特征方程的根始终满足闭环极点的定义。 二阶系统的根轨迹有以下特点： 1. 当K=0时，根轨迹从开环极点0和-a出发。 2. 对于过阻尼系统（K< a²/4），根位于负实轴上，系统响应无振荡。 3. 当K=a²/4时，根轨迹会合于点(2a, 0)，此时系统转变为临界阻尼状态，特征根为一对相等的实根。 4. 当K>a²/4时，系统进入欠阻尼状态，根轨迹将形成一对共轭复数根，产生振荡。随着K增大，振荡频率提高，但调节时间基本保持不变，因为负实部的特征根不变。 根轨迹的绘制规则包括： 1. 起点和终点：根轨迹从开环极点开始，终止于开环零点或无穷远点。 2. 实轴上的根轨迹：当K变化时，根轨迹可能与实轴相交，这些交点满足幅值条件。 3. 角度分岔：根轨迹在极点和零点附近的角度变化遵循特定规则，如180度分岔和0度分岔。 4. 轨迹方向：根轨迹通常沿顺时针或逆时针方向移动，取决于系统参数的增减。 利用根轨迹分析系统性能，我们可以预判不同参数设置下系统的稳定性、超调量、调节时间和上升时间等性能指标。这对于系统设计和优化具有重要意义，使得工程师能够通过调整系统参数来改善或满足特定的动态性能要求。