MATLAB科学计算:从一维插值到二维插值
需积分: 11 34 浏览量
更新于2024-07-26
收藏 234KB DOC 举报
"MATLAB科学计算教程"
MATLAB是一款强大的数学计算和数据分析软件,广泛应用于科研和工程领域。本文将深入探讨如何使用MATLAB进行各种科学计算任务,包括插值、曲线拟合、数值积分、数值微分、微分方程数值解、优化问题解决以及回归分析。
1. 一维插值
一维插值是确定未知点值的基本方法。在MATLAB中,`interp1`函数提供了一维插值的功能,支持多种插值方法如最近邻插值('nearest')、线性插值('linear')、三次样条插值('spline')和三次多项式插值('cubic')。例如,通过给定的数据点求解不同深度的水温,可以利用`interp1`函数实现。
2. 二维插值
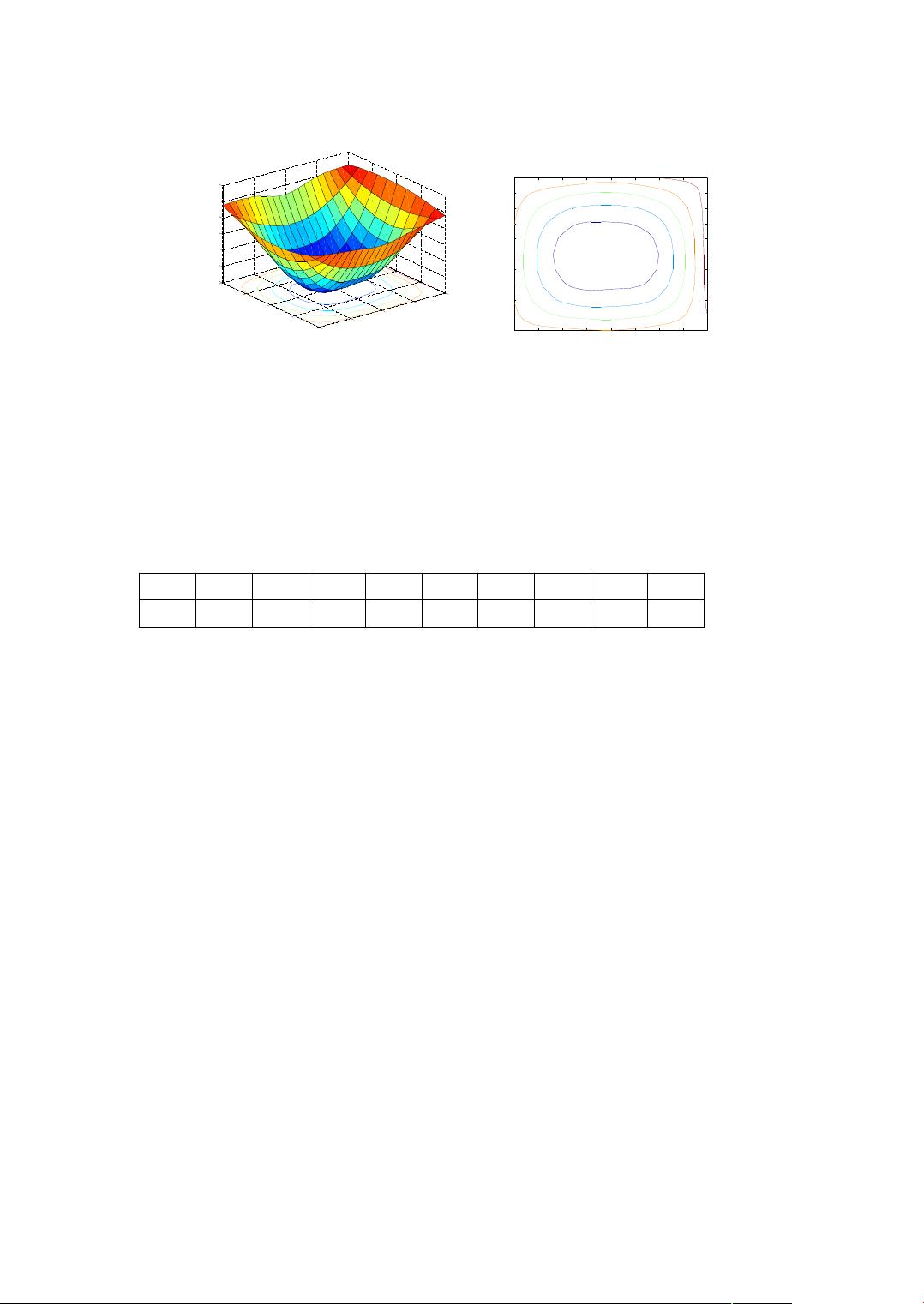
二维插值用于获取二维平面上未测量点的值。MATLAB中的`interp2`函数为此提供了解决方案。以一个金属薄片的温度分布为例,可以使用该函数进行三阶插值,然后绘制等温线图,提高数据的可视化效果。
3. 曲线拟合
MATLAB提供了多种曲线拟合工具,例如`polyfit`函数用于多项式拟合,`lsqcurvefit`用于非线性曲线拟合。通过这些工具,可以找到数据点的最佳拟合曲线。
4. 数值积分
MATLAB的`integral`或`quad`函数用于数值积分。它们可以处理定积分和不定积分问题,即使对于复杂函数也能得到近似解。
5. 数值微分
数值微分用于估算函数的导数,MATLAB的`diff`函数适用于简单的差分操作,`finitediff`可以用于更精确的有限差分方法。
6. 微分方程数值解
MATLAB的`ode45`是最常用的求解常微分方程(ODE)的函数,它采用四阶Runge-Kutta方法。此外,还有`ode23`, `ode113`等其他选项,分别适用于不同类型的微分方程和精度需求。
7. 解优化问题
MATLAB的`fmincon`和`fminunc`函数可用于解决约束或无约束优化问题,寻找函数的最小值。`lsqnonlin`和`lsqcurvefit`则用于非线性最小二乘问题。
8. 回归分析
MATLAB提供了丰富的回归分析工具,如`regress`用于线性回归,`polyfit`用于多项式回归,以及`nlinfit`用于非线性回归。这些工具可以帮助用户分析数据之间的关系,并建立预测模型。
MATLAB以其强大的计算能力,成为科学家和工程师进行复杂科学计算和数据分析的首选工具。掌握这些基本操作,将极大地提升你在科研和工程实践中的工作效率。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2023-09-18 上传
2019-08-13 上传
2008-12-12 上传
lengthc
- 粉丝: 0
- 资源: 1
最新资源
- Android应用源码利用poi将内容填到word模板-IT计算机-毕业设计.zip
- mdi-es:材料设计图标导出为ES模块
- LocationSearch
- 行业文档-设计装置-一种利用浸胶纸作为过渡联接体的胶合板.zip
- ImageProcessingApp:使用流行的MVC架构的图像处理应用程序
- hideandseek:Hide & Seek 是一款开源的多人在线街机游戏,对抗两支捉迷藏者团队,玩法有趣快节奏。 项目已从 https 移出
- angular-first-app
- 数据库课程设计-家庭理财管理.zip
- MochaBabelCoverage:一个 Mocha 运行器,支持对包含 JSX 的文件运行 Mocha,并支持覆盖率报告
- 脑机接口BCI-eeglab安装包
- grantwforsythe.github.io
- 性能测试工具LoadRunner书籍(14本)目录知识点(思维导图加图).rar
- ArgRouter:为js函数添加重载功能
- 2D形状
- android应用源码合肥工业大学客户端源码-IT计算机-毕业设计.zip
- PdfFormFillerUTF-8:带有命令行或 WWW 界面的简单 PDF Form Filler 实用程序。-开源