主成分分析PCA：降维与数据压缩方法

该资源是一个关于主成分分析(PCA)的课件，主要讲解了PCA的概念、作用、原理以及在实际中的应用，并通过Python代码展示了PCA的实现过程。 主成分分析（PCA）是一种广泛应用于数据分析领域的统计技术，主要用于解决数据高维性带来的问题，如自变量之间的多重共线性。PCA的目标是通过线性变换将原有的高维数据转换为一组各维度线性无关的新变量，即主成分，这些主成分能够最大限度地保留原始数据的信息，并且使得新变量之间的相关性尽可能小。 PCA的作用主要包括以下几点： 1. **数据降维**：通过减少特征数量来简化模型，降低计算复杂性，同时避免过拟合。 2. **噪声过滤**：主成分通常是数据变异最大的方向，可以用来去除随机噪声或不重要的信息。 3. **数据可视化**：将高维数据投影到二维或三维空间，便于观察和理解数据分布。 PCA的原理可以分为以下几个步骤： 1. **数据标准化**：确保所有特征在同一尺度上，消除量纲影响。 2. **计算协方差矩阵**：衡量特征间的相互关联程度。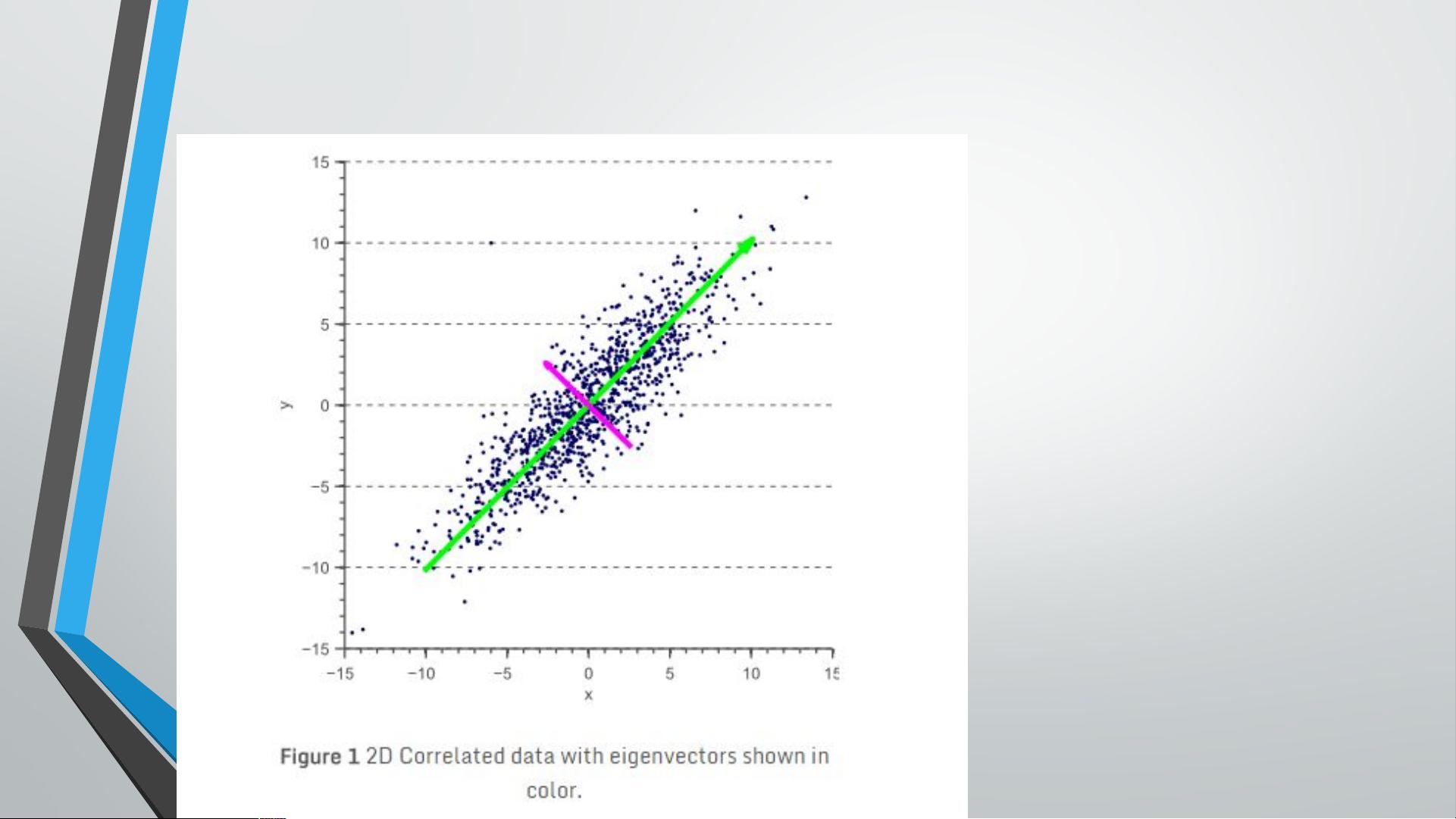 3. **求解特征值和特征向量**：特征值反映了每个特征方向上的方差大小，特征向量决定了主成分的方向。 4. **选取主成分**：根据特征值大小排序，选择前k个最大的特征值对应的特征向量，作为新的主成分。 5. **计算累积贡献率**：确定保留多少主成分能捕获大部分数据的方差。 在实践中，PCA算法有其优缺点： 优点： - **独立性**：主成分之间正交，互不相关，便于后续分析。 - **简单性**：主要涉及特征值分解，计算相对简单。 - **无参数性**：仅依赖于数据的方差，不涉及额外的假设或参数设置。 缺点： - **解释性**：主成分往往是原始特征的线性组合，它们的物理意义不如原始特征直观。 - **信息丢失**：降维可能导致部分信息丢失，特别是低方差特征可能包含重要的信息。 - **依赖数据分布**：PCA效果受数据分布影响，如果数据不满足正态分布或存在离群值，可能影响结果。 在Python中，可以使用`sklearn.decomposition.PCA`库进行PCA操作。例如，以下代码读取数据，然后使用PCA将8个特征压缩为2个主成分，并打印出贡献率： ```python import pandas as pd import matplotlib.pyplot as plt from sklearn.decomposition import PCA data = pd.read_csv('live.csv', encoding='gb2312') pca = PCA(n_components=2) pca.fit(data.iloc[:, 1:8]) newdata = pca.transform(data.iloc[:, 1:8]) print("贡献率", pca.explained_variance_ratio_) ``` 这段代码展示了如何在实际项目中运用PCA进行数据降维，`explained_variance_ratio_`属性用于查看每个主成分对总方差的贡献比例。 PCA是数据科学中一个强大且实用的工具，适用于诸多领域，包括机器学习模型的特征选择、图像压缩、生物信息学等。通过理解和应用PCA，我们可以更好地挖掘数据的潜在结构，提升模型性能，同时简化数据处理流程。