窗函数法设计FIR数字滤波器

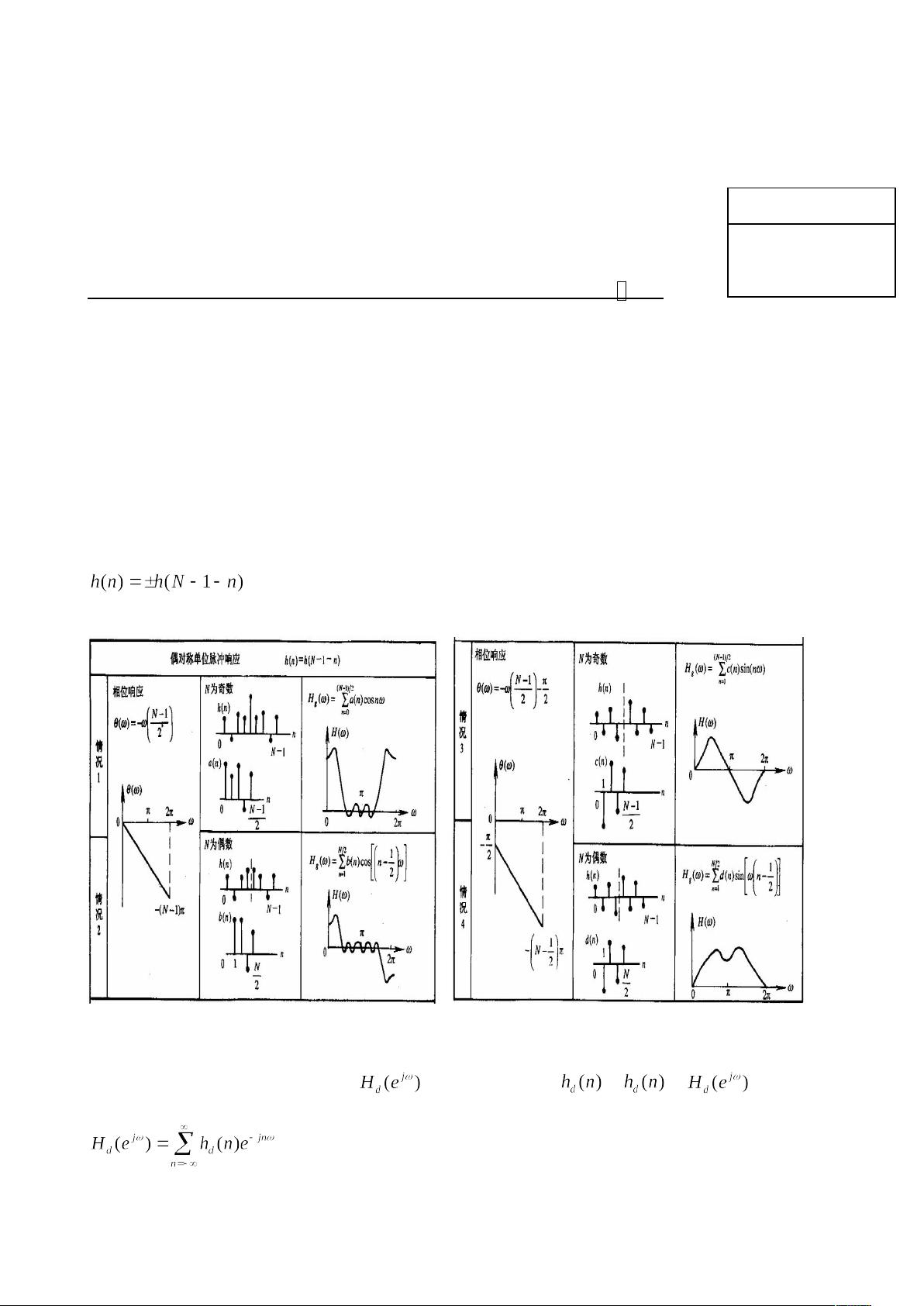
"FIR数字滤波器设计与窗函数法" 在数字信号处理领域，FIR（Finite Impulse Response，有限 impulse response）数字滤波器是一种重要的信号处理工具，尤其以其线性相位特性受到青睐。本实验旨在让学习者掌握FIR滤波器的设计方法，熟悉线性相位滤波器的特性，并了解不同窗函数对滤波性能的影响。 线性相位FIR滤波器具有以下特性：当滤波器的单位脉冲响应h(n)满足特定的对称条件时，系统可以实现严格的线性相位。这通常意味着h(n)要么是奇对称，要么是偶对称，对应于滤波器长度为奇数或偶数。根据这种对称性，线性相位FIR滤波器的幅频特性可以分为四种类型，这些特性对于设计具有特定频率响应的滤波器至关重要。 设计FIR滤波器的一种常见方法是窗函数法。首先，我们需要一个理想频率响应H(f)，然后通过傅里叶变换得到对应的单位脉冲响应h(n)。然而，这个h(n)通常是无限长且非因果的，不适合实际应用。因此，我们会对h(n)进行截断，即使用窗函数w(n)对其进行加窗处理，生成实际的有限长单位脉冲响应h'(n)。窗函数的选择和长度N将直接影响滤波器的性能，包括通带和阻带的滚降率以及过渡带的宽度。 设计线性相位FIR滤波器的步骤如下： 1. 确定滤波器的性能需求，如临界频率和单位脉冲响应长度N。 2. 根据性能需求选择h(n)的奇偶对称性，以确定理想频率响应H(f)的幅频和相频特性。 3. 计算理想单位脉冲响应h(n)。通常采用等距采样并进行逆离散傅里叶变换（IDFT）来近似H(f)。 4. 选择合适的窗函数w(n)，结合h(n)设计FIR滤波器的单位脉冲响应h'(n)。 5. 分析h'(n)的幅频特性，如果不符合要求，可以调整窗函数或N，重复设计过程。 窗函数的选择对滤波器性能有显著影响。窗函数的傅里叶变换主瓣决定了频率响应的过渡带宽，而旁瓣的大小和数量则影响通带和阻带内的波动。常见的窗函数有矩形窗、汉明窗、哈明窗、布莱克曼窗等，它们各有优缺点，适用于不同的滤波应用场景。 通过这个实验，学生不仅能够理解FIR滤波器设计的基本原理，还能通过实践掌握如何利用MATLAB等工具进行滤波器设计，并能深入探讨不同窗函数对滤波性能的具体影响，为后续的数字信号处理工作打下坚实基础。