维纳滤波与卡尔曼滤波算法详解

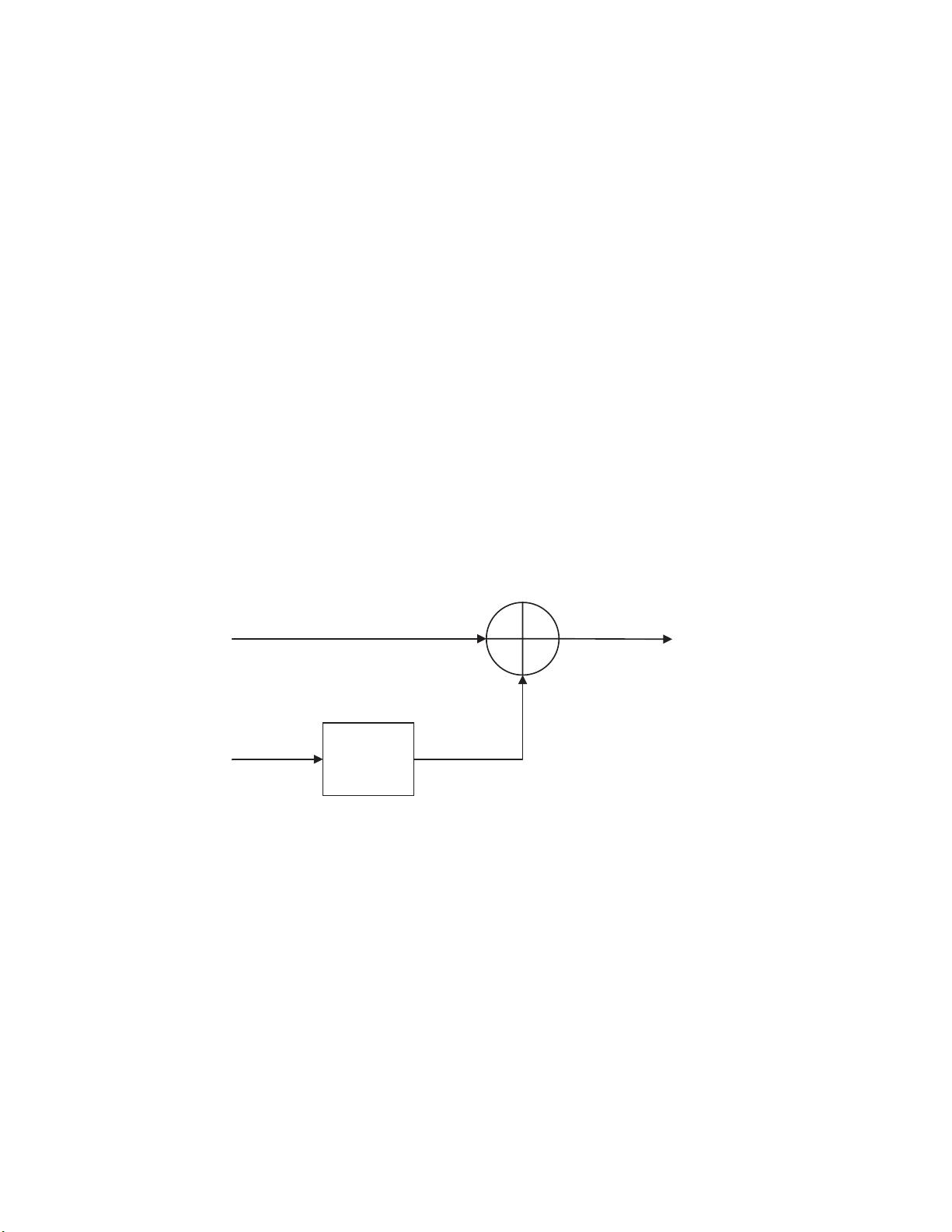
"该资源是一份关于维纳滤波与卡尔曼滤波的总结文档，由胡云博撰写。文档详细介绍了这两种滤波算法的基本思想和数学推导过程，主要适用于现代信号处理领域的学习和研究。" 正文: 维纳滤波和卡尔曼滤波是现代信号处理中的关键算法，广泛应用于噪声去除、数据预测和系统状态估计等多个领域。这篇文档首先详细阐述了维纳滤波器的工作原理和推导过程。 维纳滤波器是一种线性滤波器，其设计目标是通过调整滤波器参数，最小化输出与期望信号（参考信号）之间的均方误差。在文档中，作者给出了维纳滤波器的结构图，并解释了滤波器输入、输出以及误差信号的定义。滤波器参数向量h(n)与输入序列x(n)之间的关系被定义为一个有限阶的线性组合。为了找到最优的滤波器参数，文档介绍了使均方误差E[e²(n)]最小化的优化方法，即通过对误差的均方值关于滤波器参数h求导并令其等于零，得出最优滤波器参数h_opt的表达式：h_opt = R_xx⁻¹r_yx，其中R_xx是输入信号的自相关矩阵，r_yx是参考信号与输入信号的协相关矩阵。 文档还提到了正交原理，即最优线性滤波器的误差与输入之间互相关为零，这意味着滤波器能够有效地消除或提取输入信号中的特定成分。这一原理是设计维纳滤波器的重要依据。 接下来，文档很可能会介绍卡尔曼滤波，这是一种在线估计系统状态的递归算法，尤其适用于存在噪声的情况。卡尔曼滤波基于贝叶斯理论，结合先验知识和新测量数据，更新对系统状态的估计。其基本步骤包括预测和更新两个阶段，利用系统的动态模型和观测模型来不断优化状态估计。 卡尔曼滤波器的关键在于卡尔曼增益，它决定了如何权衡预测和观测信息。通过适当计算卡尔曼增益，可以实现对系统状态估计的最小均方误差。在实际应用中，卡尔曼滤波常用于导航、控制工程、图像处理等领域。 总结来说，这篇文档深入探讨了维纳滤波和卡尔曼滤波的基本理论，对于理解这两种滤波算法的原理和应用具有很高的价值。无论是初学者还是经验丰富的工程师，都能从中受益，提升对现代信号处理技术的理解。