LINGO数学建模软件完全指南

"LINGO教程大全文档" LINGO（Linear Interactive and General Optimization）是一款强大的数学建模软件，专用于解决各种优化问题。本教程详细介绍了LINGO在优化模型构建和求解中的应用。 1.1优化模型的基本概念 在优化模型中，基本概念包括决策变量、目标函数和约束条件。决策变量是模型中可以调整的参数，通常代表了系统中的未知量。目标函数是需要优化的目标，可能是最大化或最小化某个指标。约束条件则是对决策变量的限制，确保模型的解决方案符合实际问题的限制要求。优化模型的一般形式可以表示为：最大化/最小化目标函数，同时满足一组线性和/或非线性的约束条件。 1.1.1优化模型的一般形式 一个典型的优化模型通常包含以下部分： - 目标函数：定义我们希望最大化或最小化的量。 - 决策变量：模型中需要确定的未知数，它们的取值直接影响到目标函数的结果。 - 约束条件：对决策变量的限制，可以是等式或不等式形式，确保模型的解具有实际意义。 - 界限：对决策变量可能的取值范围进行界定。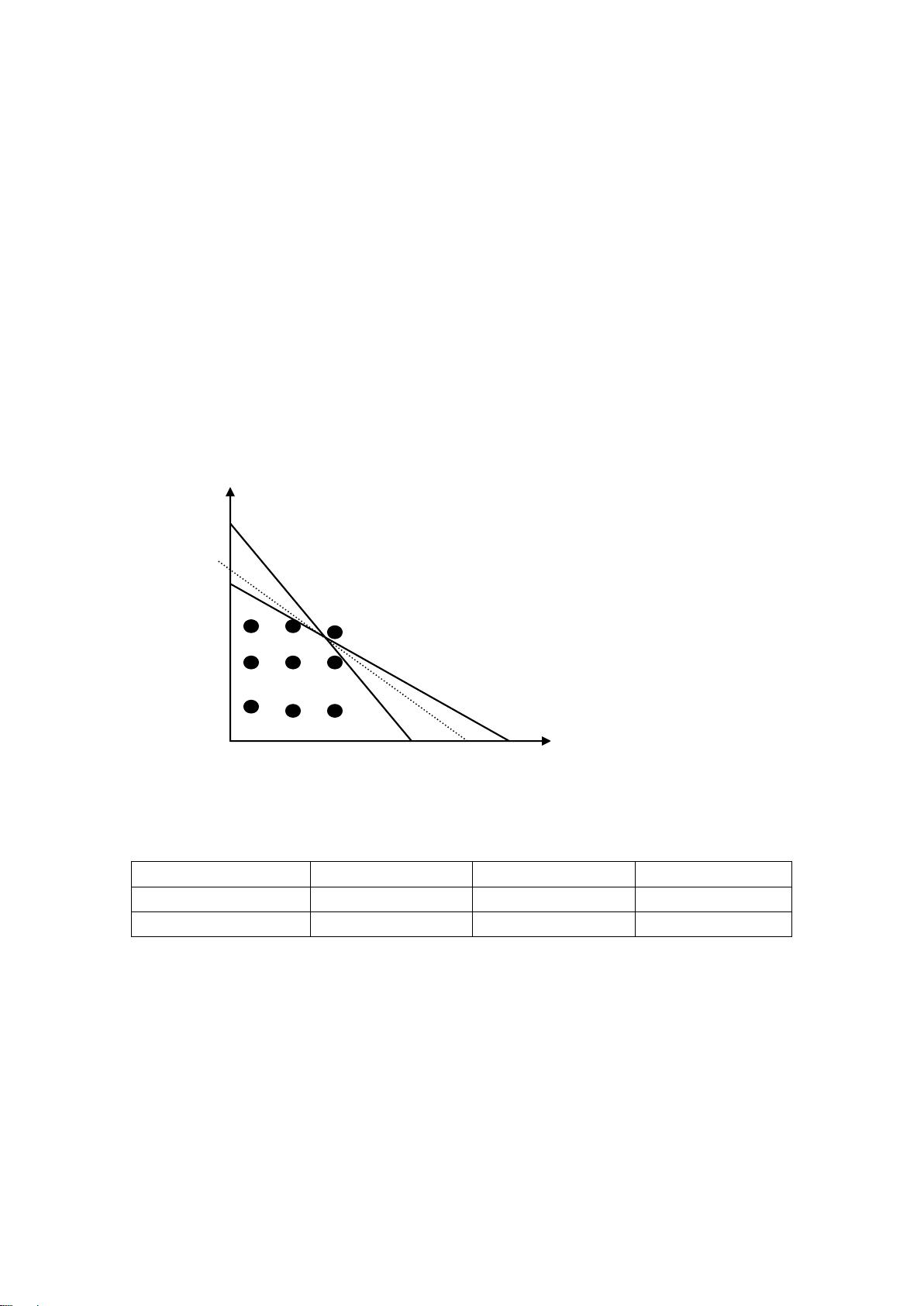 1.1.2可行解与最优解 可行解是指满足所有约束条件的决策变量组合，而最优解是所有可行解中使目标函数达到最优（最大值或最小值）的解。在有多个可行解时，我们需要找到使得目标函数最优的那个。 1.1.3优化模型的基本类型 优化模型根据目标函数和约束条件的特性，主要分为以下几类： - 线性规划：目标函数和约束条件都是线性的。 - 二次规划：目标函数是二次函数，约束条件可以是线性的或二次的。 - 非线性规划：目标函数或约束条件至少有一个是非线性的。 - 整数规划：决策变量必须取整数值，常用于处理包含“是/否”决策的问题。 - 混合整数规划：结合了连续决策变量和整数决策变量。 1.2优化问题的建模实例 1.2.1线性规划模型 线性规划是最基础的优化模型，广泛应用于生产计划、运输问题等领域。例如，通过调整生产量来最大化利润，同时满足生产能力、原材料供应等约束。 1.2.2二次规划模型 二次规划模型适用于处理目标函数为二次函数的问题，如投资组合优化、能源管理等。它的特点是目标函数是平方项的加权和。 1.2.3非线性规划模型 非线性规划模型涵盖了更广泛的优化问题，例如在成本函数中存在非线性项，或者约束条件涉及非线性关系。 1.2.4整数规划模型 整数规划在物流、调度等问题中非常常见，如员工排班、项目分配等。它要求某些决策变量只能取整数值。 1.2.5其他优化模型 除了以上几种，还有许多其他类型的优化模型，如动态规划、随机规划、多目标优化等，它们各自适用于不同的问题领域，LINGO都能有效地支持这些模型的建立和求解。 通过LINGO，用户可以方便地构建各种复杂优化模型，利用其内置的高效求解器找到最优解，从而解决实际问题。无论是学术研究还是工业应用，LINGO都是一款不可或缺的工具。