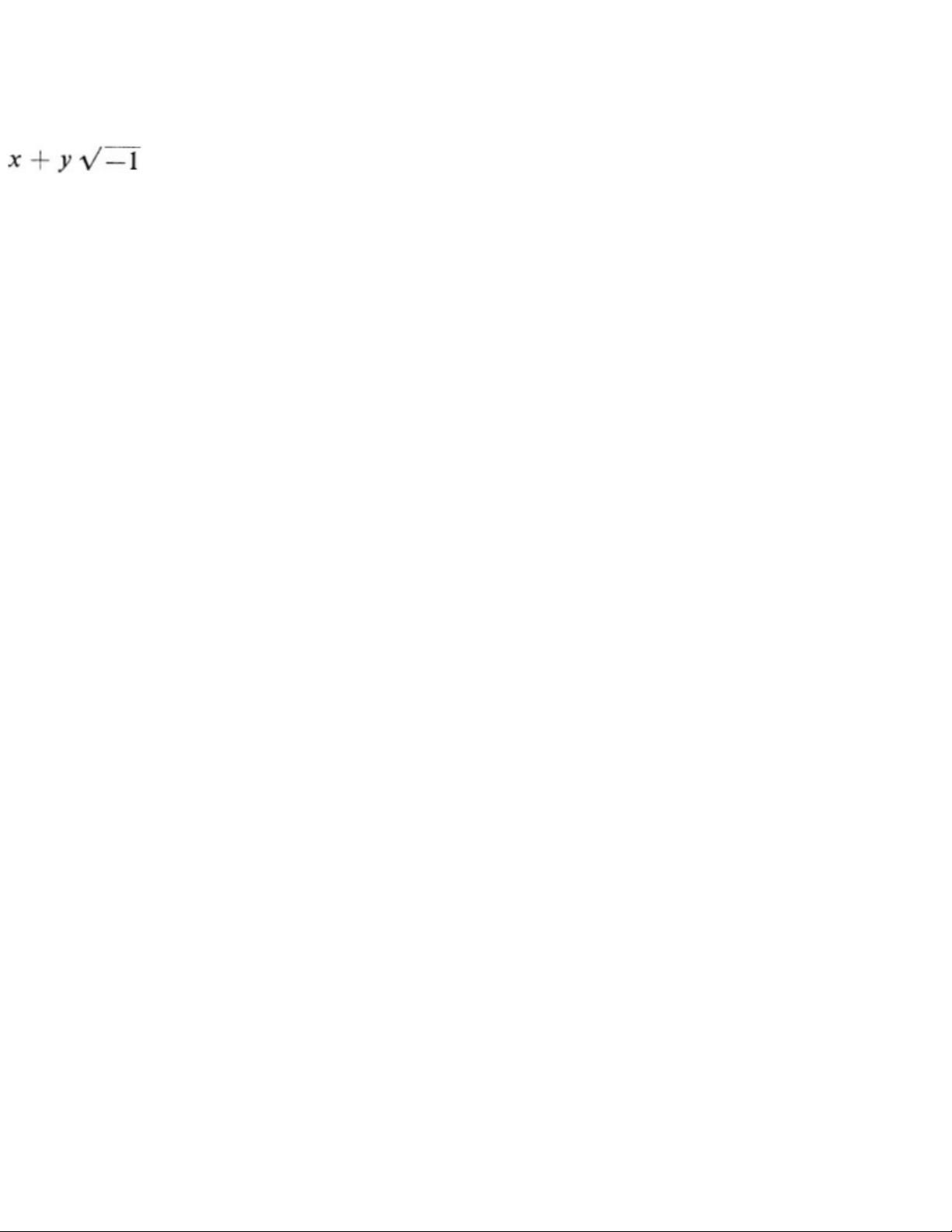single technical process which can be carried through without more or less complicated calculations;
and mathematics plays a very important role in the development of new branches of technology.
Finally, it is true that every science, to a greater or lesser degree, makes essential use of
mathematics. The “exact sciences,” mechanics, astronomy, physics, and to a great extent chemistry,
express their laws, as every schoolboy knows, by means of formulas and make extensive use of
mathematical apparatus in developing their theories. The progress of these sciences would have been
completely impossible without mathematics. For this reason the requirements of mechanics,
astronomy, and physics have always exercised a direct and decisive influence on the development of
mathematics.
In other sciences mathematics plays a smaller role, but here too it finds important applications. Of
course, in the study of such complicated phenomena as occur in biology and sociology, the
mathematical method cannot play the same role as, let us say, in physics. In all cases, but especially
where the phenomena are most complicated, we must bear in mind, if we are not to lose our way in
meaningless play with formulas, that the application of mathematics is significant only if the concrete
phenomena have already been made the subject of a profound theory. In one way or another,
mathematics is applied in almost every science, from mechanics to political economy.
Let us recall some particularly brilliant applications of mathematics in the exact sciences and in
technology.
The planet Neptune, one of the most distant in the Solar System, was discovered in the year 1846
on the basis of mathematical calculations. By analyzing certain irregularities in the motion of Uranus,
the astronomers Adams and Leverrier came to the conclusion that these irregularities were caused by
the gravitational attraction of another planet. Leverrier calculated on the basis of the laws of
mechanics exactly where this planet must be, and an observer to whom he communicated his results
caught sight of it in his telescope in the exact position indicated by Leverrier. This discovery was a
triumph not only for mechanics and astronomy, and in particular for the system of Copernicus, but also
for the powers of mathematical calculation.
Another example, no less impressive, was the discovery of electromagnetic waves. The English
physicist Maxwell, by generalizing the laws of electromagnetic phenomena as established by
experiment, was able to express these laws in the form of equations. From these equations he
deduced, by purely mathematical methods, that electromagnetic waves could exist and that they must
be propagated with the speed of light. On the basis of this result, he proposed the electromagnetic
theory of light, which was later developed and deepened in every direction. Moreover, Maxwell’s
results led to the search for electromagnetic waves of purely electrical origin, arising for example
from an oscillating charge. These waves were actually discovered by Hertz. Shortly afterwards, A. S.
Popov. by discovering means for exciting, transmitting, and receiving electromagnetic oscillations
made them available for a wide range of applications and thereby laid the foundations for the whole
technology of radio. In the discovery of radio, now the common possession of everyone, an important
role was played by the results of a purely mathematical deduction.
So from observation, as for example of the deflection of a magnetic needle by an electric current,
science proceeds to generalization, to a theory of the phenomena, and to formulation of laws and to
mathematical expression of them. From these laws come new deductions, and finally, the theory is
embodied in practice, which in its turn provides powerful new impulses for the development of the
theory.
It is particularly remarkable that even the most abstract constructions of mathematics, arising
within that science itself, without any immediate motivation from the natural sciences or from