正态分布详解：概念、特点和应用

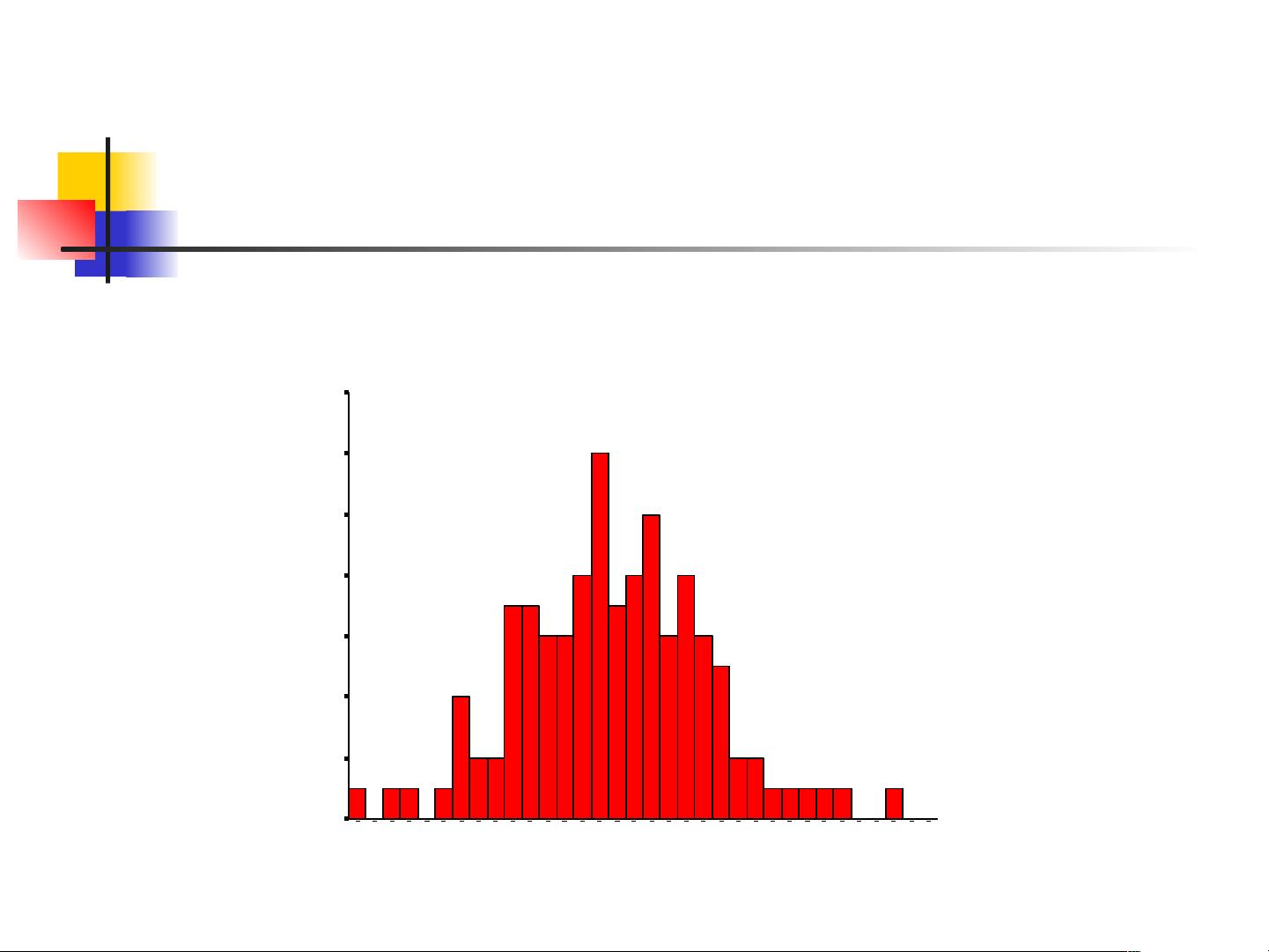
正态分布详解 正态分布是概率论和统计学中的一种重要概念，它是指一组数据的分布呈现中间多，两侧对称的特征。下面我们将详细介绍正态分布的概念、特征、应用以及在数学和统计学中的重要性。 一、正态分布的概念 正态分布是一种连续型概率分布，它是由 Carl Friedrich Gauss 在 19 世纪初期提出。正态分布也被称为高斯分布或常态分布，它是根据概率论和统计学的理论推断，描述了随机变量的分布规律。 二、正态分布的特征 正态分布的特征是它的概率密度函数呈现钟形曲线，中间多，两侧对称。这个曲线可以用数学公式来描述： f(x) = (1/σ√(2π)) \* e^(-((x-μ)^2)/(2σ^2)) 其中，x 是随机变量，μ 是总体均数，σ 是总体标准差，π 是圆周率，e 是自然对数的底。 正态分布的特征还包括： * 对称性：正态分布的概率密度函数关于均数对称。 * 单峰性：正态分布的概率密度函数只有一个峰值，即均数。 * 连续性：正态分布的概率密度函数是连续的。 三、正态分布的应用 正态分布有着广泛的应用领域，包括： * 统计学：正态分布是统计学中最重要的分布之一，广泛应用于假设检验、confidence interval 等。 * 数据分析：正态分布可以用来描述和分析数据的分布，例如身高、体重、成绩等。 * 工程学：正态分布可以用来描述和分析工程系统中的随机变量，例如机械零件的尺寸、材料强度等。 * 医学：正态分布可以用来描述和分析生物医学中的随机变量，例如血压、身高、体重等。 四、正态分布在数学和统计学中的重要性 正态分布在数学和统计学中扮演着非常重要的角色，它是许多统计模型和方法的基础，例如： * t 检验：正态分布是 t 检验的基础，用于比较两个样本的均数。 * ANOVA 分析：正态分布是 ANOVA 分析的基础，用于比较多个样本的均数。 * 回归分析：正态分布是回归分析的基础，用于描述变量之间的关系。 正态分布是数学和统计学中的一种重要概念，它广泛应用于各种领域，了解正态分布的概念、特征和应用是非常重要的。