差分进化算法详解与应用

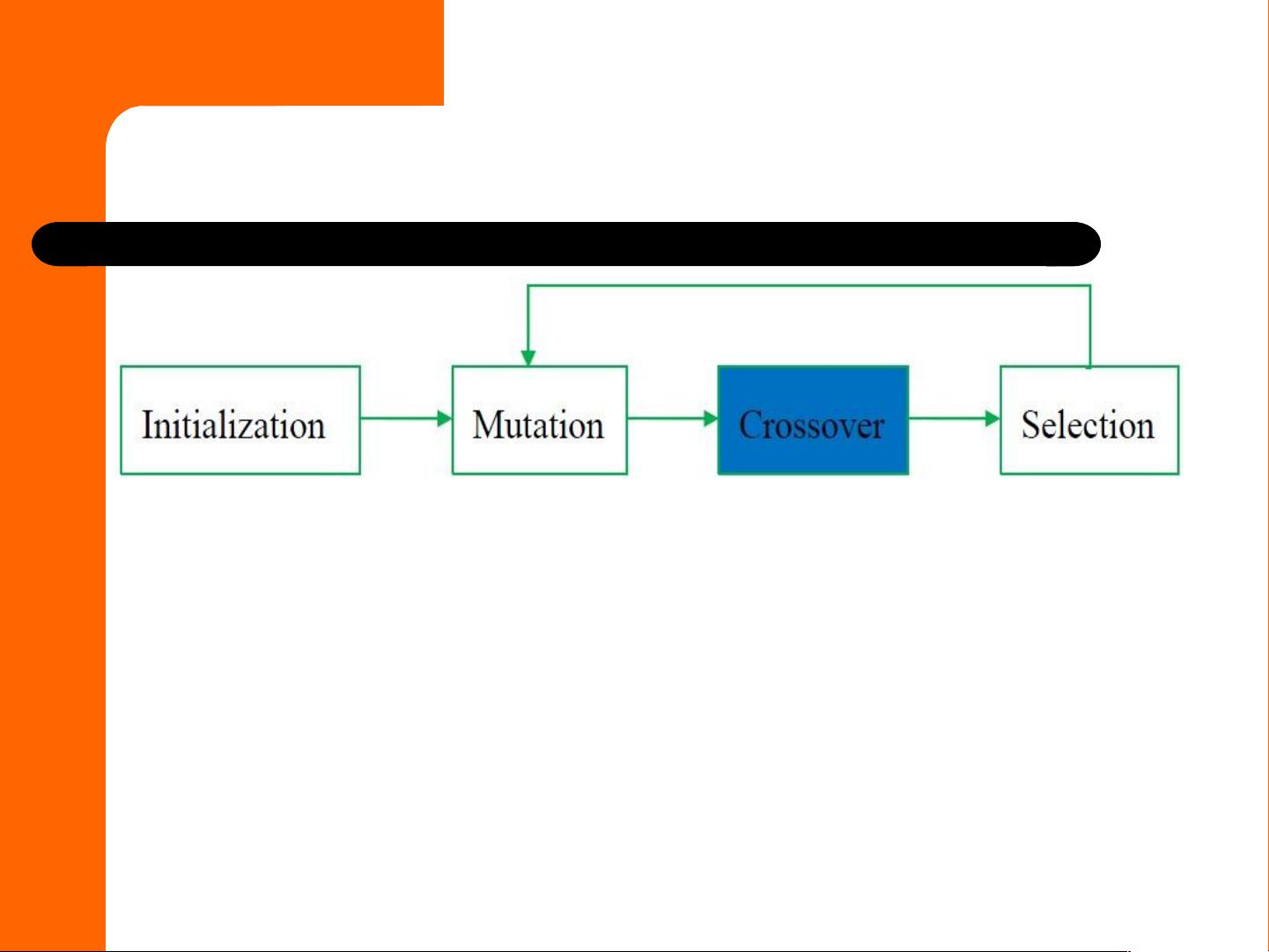
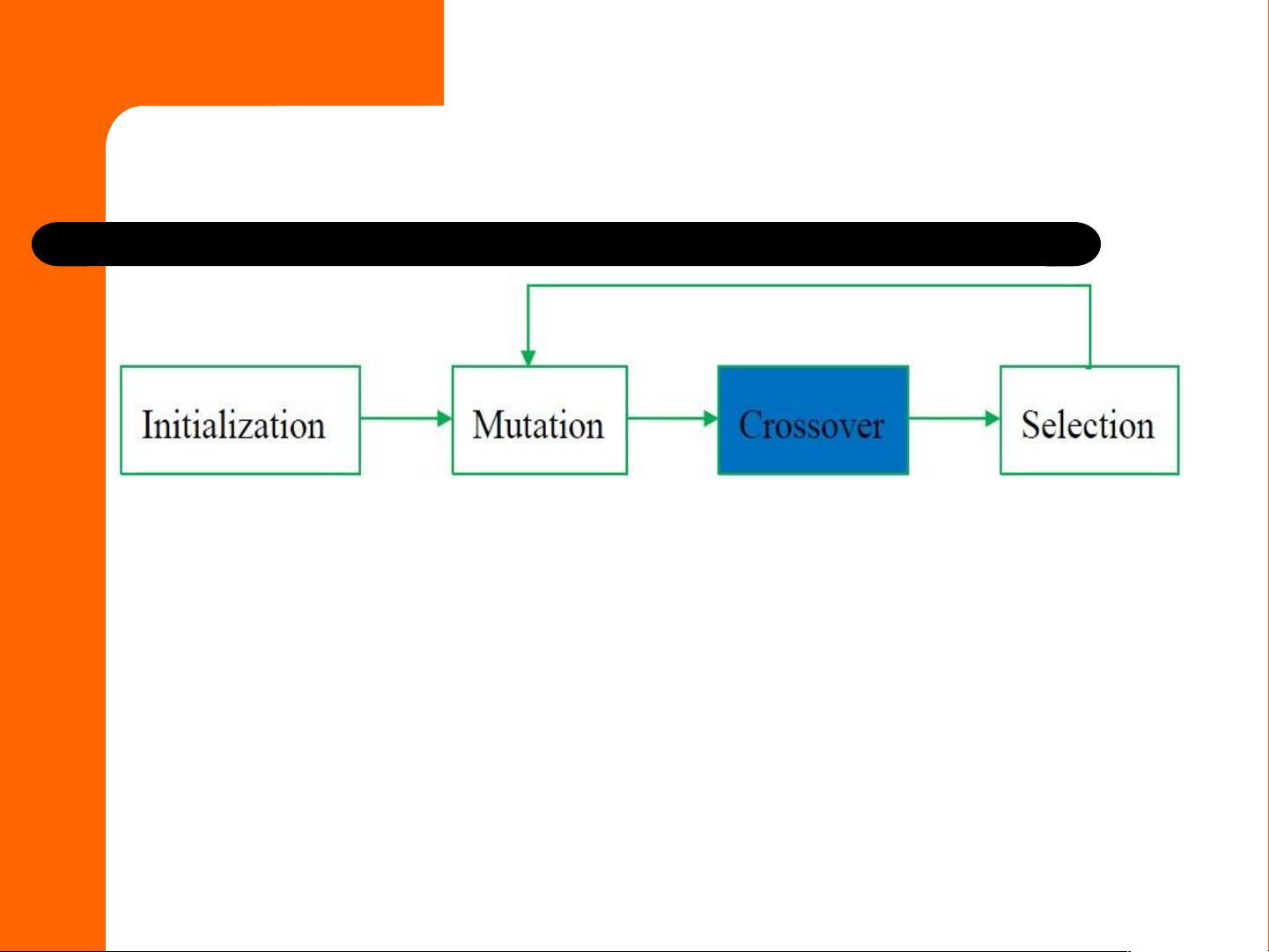
"差分算法ppt - 最近的发展方向和各种变种的介绍" 差分进化（Differential Evolution, DE）是一种强大的全局优化算法，起源于肯·普莱斯（Ken Price）在解决由莱纳尔·斯托恩（Rainer Storn）提出的切比雪夫多项式拟合问题时的尝试。这个算法的核心思想是通过向量差异来扰动种群中的向量，这一创新性的想法经过肯和莱纳尔之间的深入讨论、反复的思考以及大量的计算机模拟，最终形成了现今我们所熟知的具有灵活性和鲁棒性的差分进化算法。 差分进化属于进化算法的一种，这个类别还包括遗传算法（Genetic Algorithms, GA）、进化策略（Evolutionary Strategies）和进化编程（Evolutionary Programming）。这些算法的主要阶段通常包括初始化、选择、交叉和变异等步骤。 1. 差分进化的基本流程： - **初始化**：随机生成初始种群。 - **选择**：根据适应度函数，选择一部分个体进行后续操作。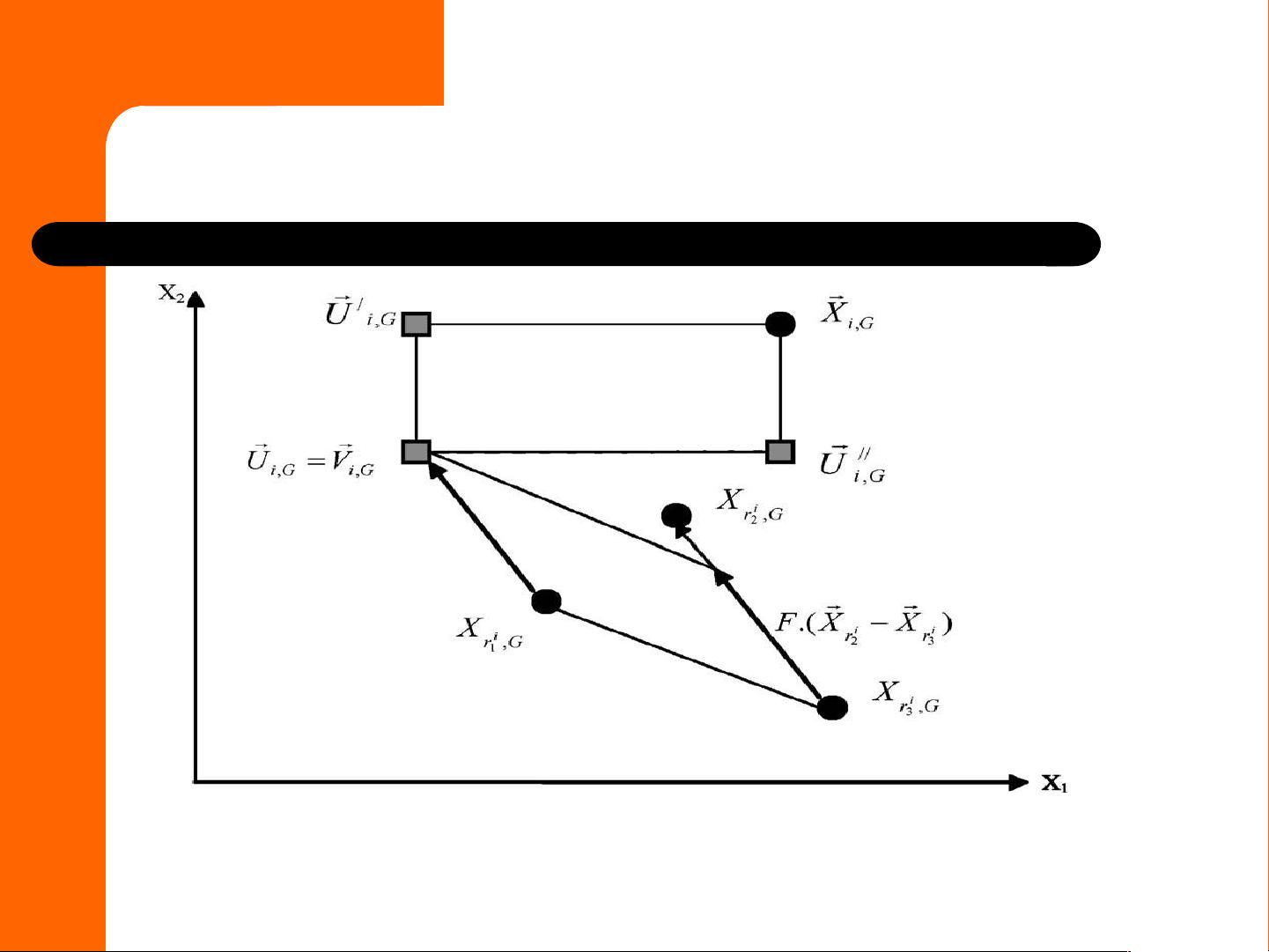 - **交叉**（变异）：通过差分操作产生新的候选解，即对三个父代向量进行操作，形成一个变异向量。 - **混合**：将变异向量与原始向量结合，可能通过简单替换或线性组合等方式。 - **评估**：计算新解的适应度值。 - **迭代**：重复以上步骤，直到满足停止条件（如达到最大迭代次数、目标精度等）。 2. 差分进化的变种： - **单目标优化问题**：针对单个目标函数的优化，有多种策略来改进搜索效率和收敛速度，如DE/best/1/bin、DE/rand/1/bin等。 - **多模态优化问题**：处理具有多个局部最优解的问题，采用全局搜索策略，如DE/current-to-best/1/bin和DE/current-to-pbest/1/bin。 - **约束优化问题**：在满足特定约束条件下求解，可以采用罚函数法或者直接处理约束的策略。 - **动态优化问题**：针对变化环境中的优化，需要算法能够快速适应变化，如自适应差分进化。 - **多目标优化问题**：处理多个相互冲突的目标函数，如NSGA-II（非支配排序遗传算法II）与DE的结合。 差分进化的优点在于其简单性和鲁棒性，能在许多复杂优化问题上表现出良好的性能。然而，它也有一些缺点，比如可能会过度探索导致收敛慢，或者在某些情况下可能出现早熟现象。因此，研究者们不断提出新的变种和策略来改善这些问题，以提高DE在不同领域的应用效果。 差分进化算法在工程优化、机器学习参数调优、控制问题、金融模型优化等领域有广泛的应用。通过理解并掌握DE的基本原理和变种，我们可以更好地利用这一工具解决实际问题，提升优化效率。