最小二乘法预测与梯度下降法求解：2014年房价预测与归一化

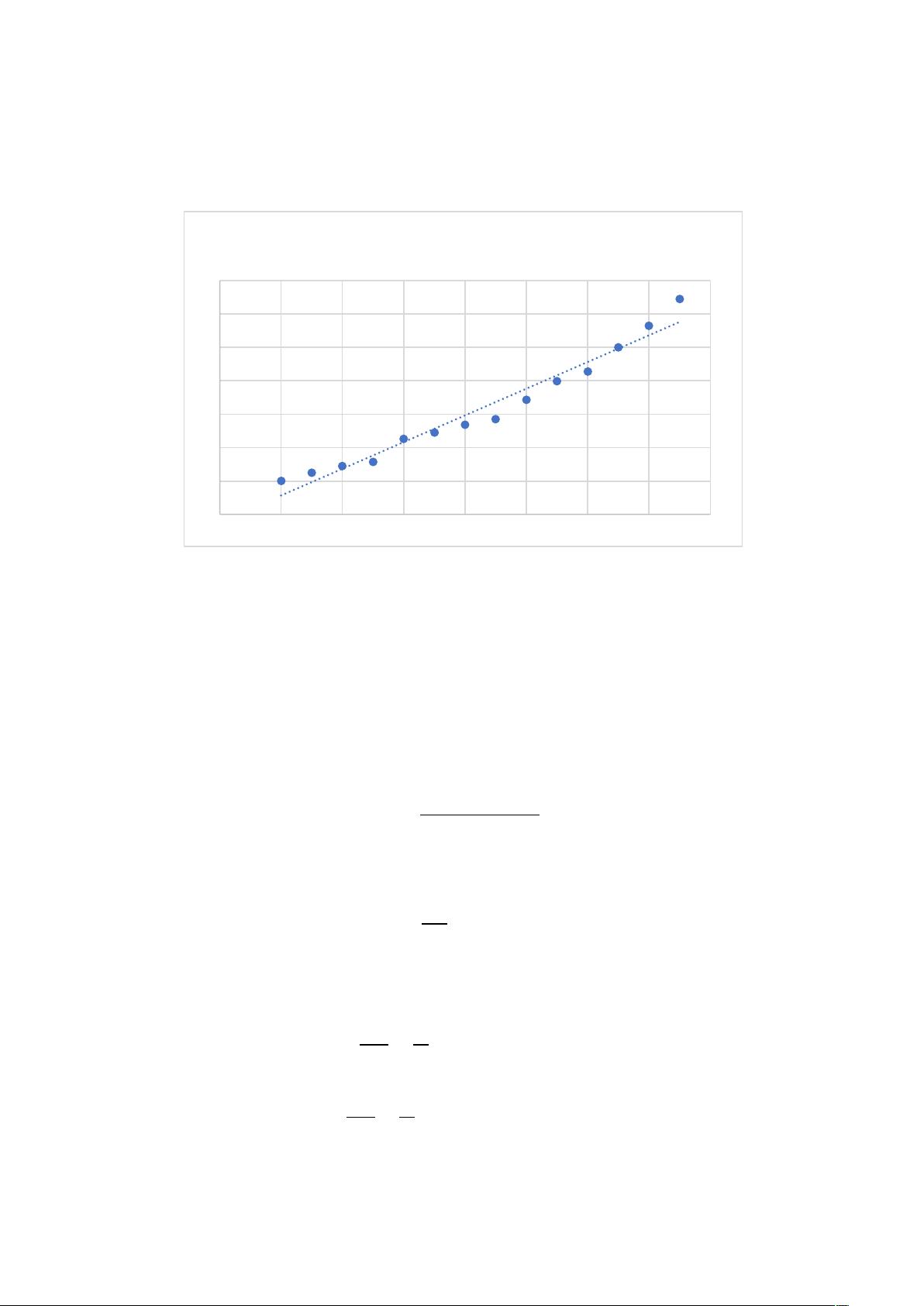
本次资源是关于黄海浪教授在机器学习课程中的第二次作业，主要涉及两个关键部分：最小二乘法预测房价和梯度下降法进行数据归一化与模型求解。 1. **最小二乘法预测**： 在这个部分，学生使用了最小二乘法来预测2014年的房价。通过拟合数据点（如时间序列数据，1998年至2014年房价），找到一条直线（y = 0.799x - 1596.9）来最接近所有数据点的平均距离。这方法假设数据点和预测线之间存在线性关系。通过计算成本函数（平方误差的平均值），即cost = 1/2m²(h(x) - y)，学生得到了预测值12.2862，表明模型认为在2014年，根据当前趋势，房价大约会达到这个数值。 2. **梯度下降法求解与归一化**： 梯度下降算法被用来优化模型参数（这里是θ0和θ1）。首先，学生将特征变量x进行了归一化处理，目的是加速梯度下降法的收敛速度，防止权重过大或过小影响学习效果。归一化公式是将每个特征值映射到0到1的范围内，即𝑥′=(𝑥−min(x))/(max(x)−min(x))。梯度推导出∂J/∂θ0和∂J/∂θ1，表明目标是减小成本函数J对参数的偏导数。经过一系列迭代（每次迭代α=0.01），学生计算并更新了θ0和θ1的值，分别得到归一化后的θ0%和θ1%，反归一化后得到用于预测的θ0和θ1。 迭代过程显示了从原始参数到最终优化参数的变化，以及对2014年房价的预测值，即12.318714687080956。这是通过梯度下降法训练得到的模型对目标变量的预测结果。 3. **代码实现**： 提供的Python代码展示了如何实际操作这些概念。它首先读取名为"data.csv"的CSV文件，从中获取输入变量x和目标变量y。然后，通过导入必要的库（如numpy和matplotlib）构建最小二乘模型和梯度下降算法。代码中定义了读取数据、计算成本函数、梯度更新以及绘图展示数据和预测结果的函数，展示了将理论应用到实践中的过程。 这份作业涵盖了机器学习中的基础模型建立（最小二乘法）、数据预处理（归一化）以及优化算法（梯度下降）的实际运用，旨在帮助学生深入理解模型构建和参数调整的方法。通过这个过程，学生能够掌握如何用数学模型解释房价变化，并通过编程实现模型的训练和预测。