傅里叶变换解析：从理论到实践

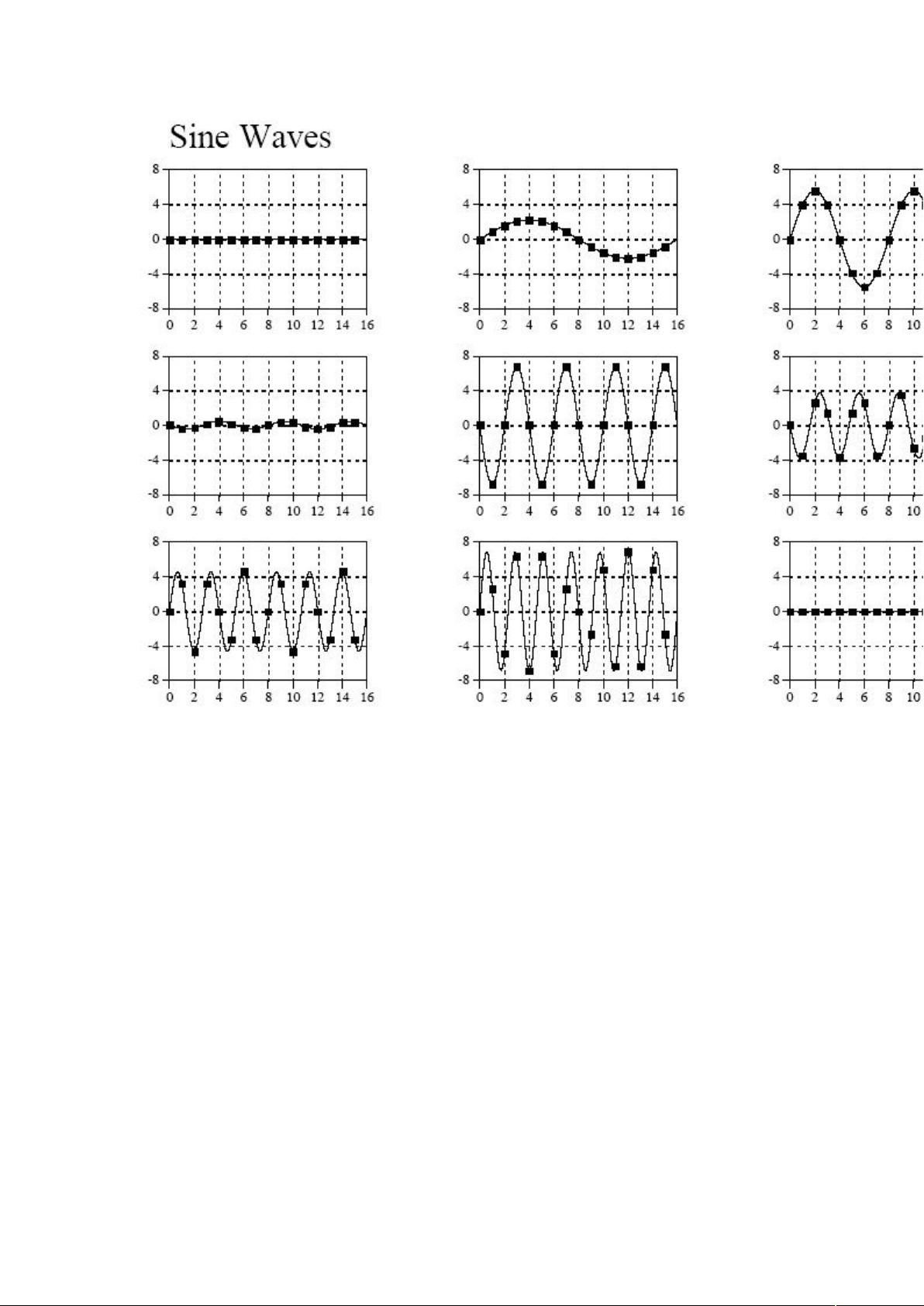
"这篇文档深入探讨了傅里叶变换，特别是离散傅立叶变换（DFT），旨在帮助读者从感性上理解这一概念。文档来源于Steven W. Smith的电子书籍，书中用易于理解的方式介绍了傅立叶变换的理论和应用。" 傅里叶变换是一种在信号处理和数学中广泛使用的工具，它将一个函数或信号从时域或空间域转换到频域，揭示了信号的频率成分。离散傅立叶变换（DFT）是傅里叶变换的离散形式，特别适用于处理数字信号。 傅立叶变换的由来可以追溯到19世纪初，由法国数学家和物理学家Jean Baptiste Joseph Fourier提出。他发现任何连续周期信号都可以表示为无限个正弦波的线性组合，这一理论在热传递的研究中尤为关键。尽管最初受到了拉格朗日等著名数学家的质疑，傅立叶的理论最终被证明是正确的，并对后续的科学和工程领域产生了深远影响。 理解傅立叶变换需要一定的数学基础，特别是级数和复数的概念。傅立叶变换的基本公式表明，一个信号可以分解为不同频率的正弦波分量。对于离散傅立叶变换，它定义了一种计算序列频谱的方法，即通过计算一系列复数的指数函数乘积来得到信号的频域表示。 离散傅立叶变换的应用广泛，包括音频和图像的编码与解码、滤波器设计、频谱分析以及通信系统中的信号处理等。在数字信号处理中，快速傅立叶变换（FFT）是一种高效的算法，用于计算DFT，极大地降低了计算复杂度。 通过学习和理解傅里叶变换，工程师和科学家能够分析信号的频率成分，从而优化通信系统的性能、降噪、识别信号特征，甚至在图像处理中进行频域滤波等。在实际应用中，例如在音频编辑软件中，我们可以直观地看到音频信号的频谱，这正是傅里叶变换的结果。 傅里叶变换是理解和处理周期性信号的关键工具，其离散形式在现代数字世界中扮演着至关重要的角色。通过深入学习和实践，我们可以更好地掌握这一强大的分析方法，解决各种领域的复杂问题。