几何问题的代数解法——吴方法与多层感知器的BP算法

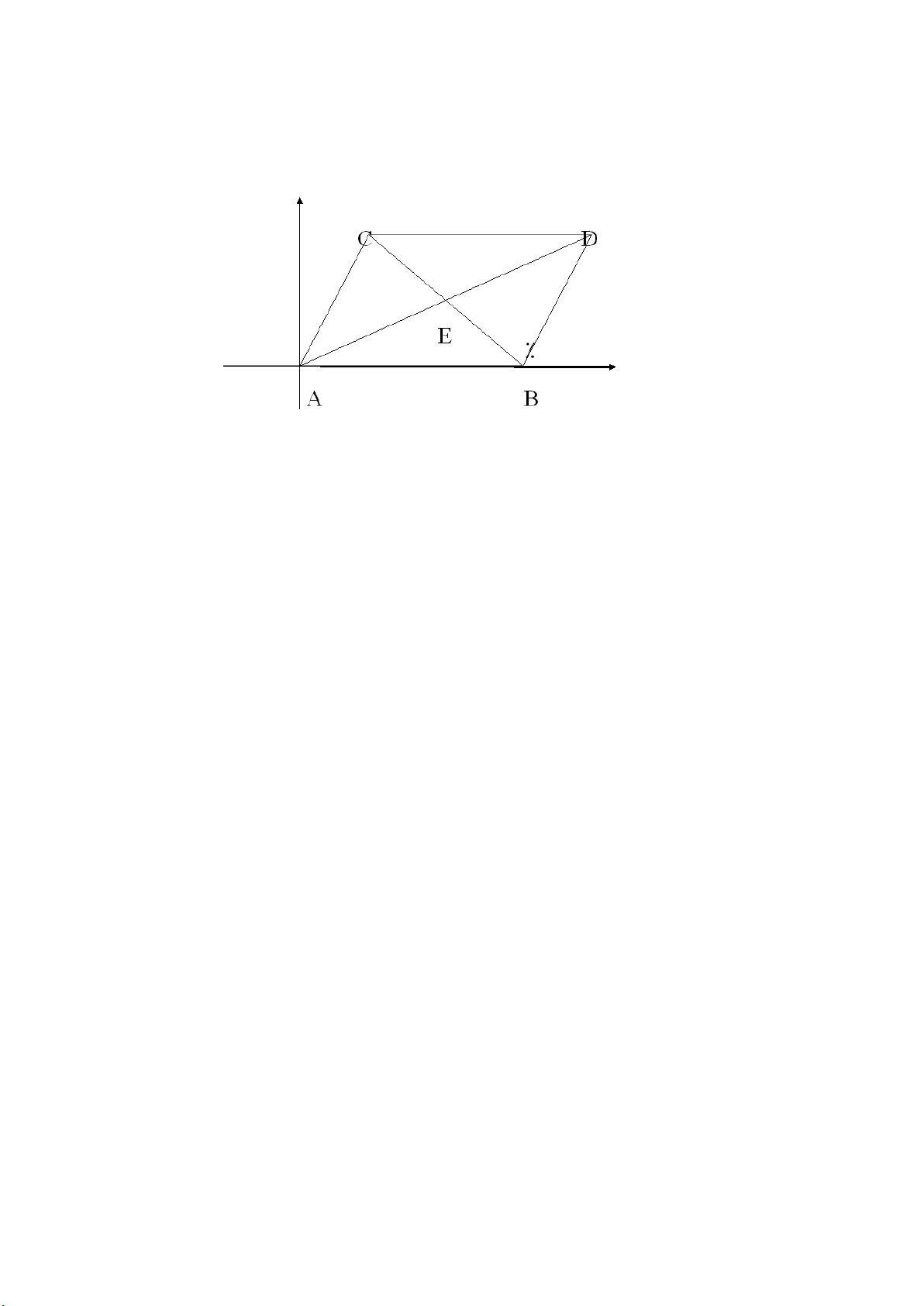
"这是一份来自武汉大学计算机学院的认知过程信息处理课程的思考题及答案，涵盖了将几何问题转化为代数问题、吴方法求解几何问题的步骤与思想、多项式带余除法、博弈论中的博弈树构建以及多层感知器的反向传播算法的应用。" 在这份资料中，我们可以深入探讨以下几个重要的知识点： 1. 几何问题的代数转化：问题一展示了如何将几何问题转化为代数问题。在平面几何中，平行线的性质可以转化为代数方程。例如，AB平行CD意味着它们的斜率相等，这可以转化为Y2=y3。通过这种方式，我们可以利用代数方法来证明或解决几何问题。 2. 吴方法：这是一种将几何问题转换为代数证明的方法，其核心思想是将几何条件和结论用代数多项式表示，然后通过代数运算来判断命题的真假。主要步骤包括多项式表达、确定变量、三角化和逐步消除约束变量。这种方法提供了一种系统化的解决几何问题的途径。 3. 多项式带余除法：问题三中提到了如何进行带余除法来简化问题。在这里，我们通过乘以适当的因子并相加，然后标准化多项式，最终得到一个关于x4的一元多项式。这是代数学中处理多项式关系和简化表达式的一种常见技巧。 4. 博弈理论：问题四涉及构建博弈树来分析博弈问题。在给定的例子中，两个玩家轮流划分7个钱币，直到对方无法继续划分为止。博弈树是一种图形工具，用于可视化所有可能的游戏结果和策略，帮助理解游戏的动态和胜利条件。 5. 反向传播算法：问题五提到了多层感知器的权重更新公式，这是神经网络学习的基础。反向传播利用梯度下降优化权重，以最小化损失函数（这里是误差平方函数）。Sigmoid函数作为激活函数，使得输出值在0到1之间连续变化，适应分类问题。通过计算误差的梯度，可以反向传播更新每一层的权重，使得网络能够逐渐学习和改进。 这些知识点展示了从基础数学概念到高级计算方法的广泛应用，对于理解和解决计算机科学中的问题至关重要。无论是几何问题的代数解决，还是神经网络的学习机制，都需要深厚的数学基础和逻辑推理能力。