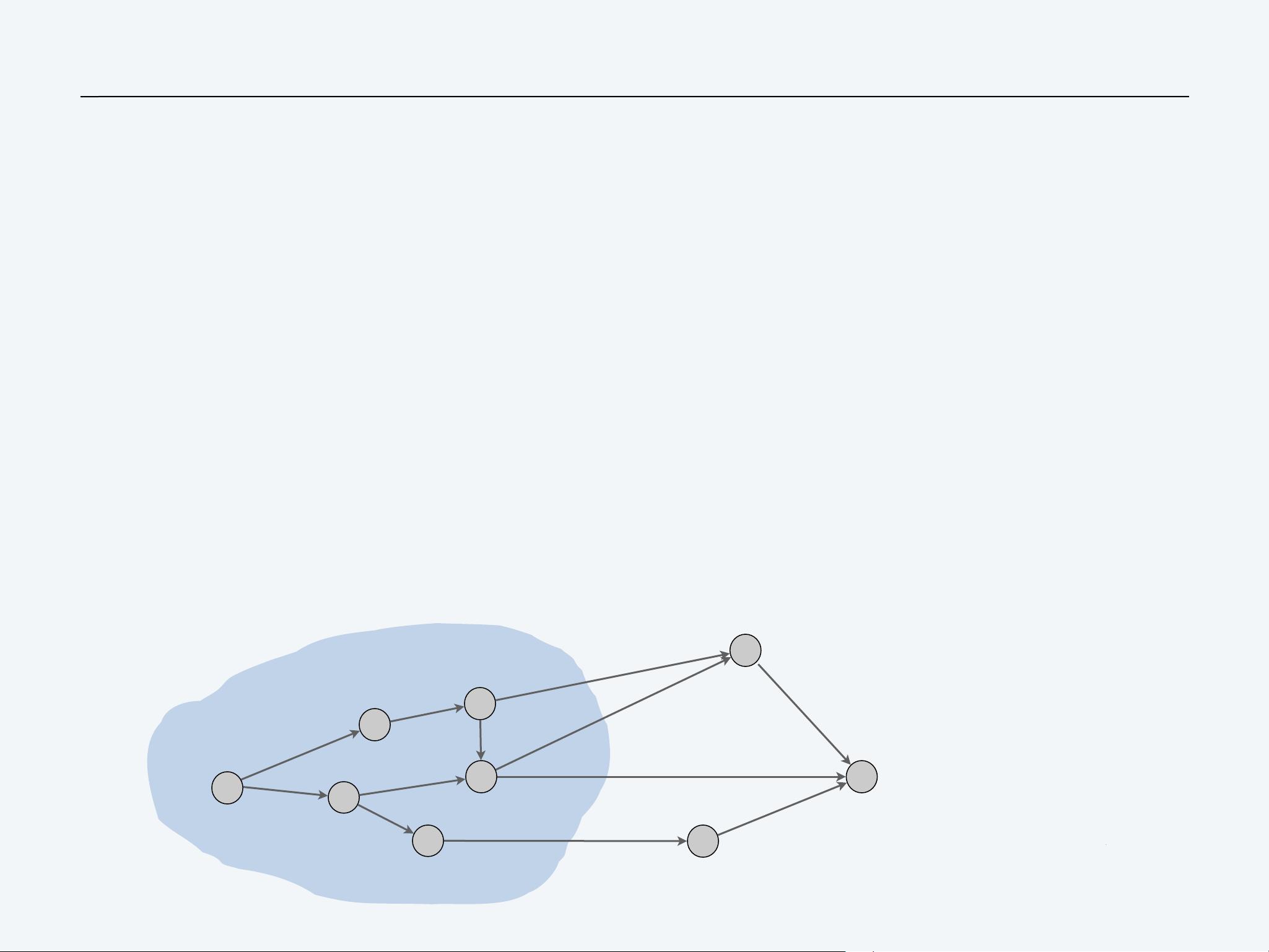
Extensions of Dijkstra’s algorithm
Dijkstra’s algorithm and proof extend to several related problems:
・
Shortest paths in undirected graphs: π[v] ≤ π[u] + ℓ(u, v).
・
Maximum capacity paths: π[v] ≥ min { π[u], c(u, v) }.
・
Maximum reliability paths: π[v] ≥ π[u] 𐄂 γ(u, v) .
・
…
Key algebraic structure. Closed semiring (min-plus, bottleneck, Viterbi, …).
16
S
π[u]
ℓ
e
Fun with Semirings
A functional pearl on the abuse of linear algebra
Stephen Dolan
Computer Laboratory, University of Cambridge
stephen.dolan@cl.cam.ac.uk
Abstract
Describing a problem using classical linear algebra is a very well-
known problem-solving technique. If your question can be formu-
lated as a question about real or complex matrices, then the answer
can often be found by standard techniques.
It’s less well-known that very similar techniques still apply
where instead of real or complex numbers we have a closed semir-
ing, which is a structure with some analogue of addition and multi-
plication that need not support subtraction or division.
We define a typeclass in Haskell for describing closed semir-
ings, and implement a few functions for manipulating matrices and
polynomials over them. We then show how these functions can
be used to calculate transitive closures, find shortest or longest
or widest paths in a graph, analyse the data flow of imperative
programs, optimally pack knapsacks, and perform discrete event
simulations, all by just providing an appropriate underlying closed
semiring.
Categories and Subject Descriptors D.1.1 [Programming Tech-
niques]: Applicative (Functional) Programming; G.2.2 [Discrete
Mathematics]: Graph Theory—graph algorithms
Keywords closed semirings; transitive closure; linear systems;
shortest paths
1. Introduction
Linear algebra provides an incredibly powerful problem-solving
toolbox. A great many problems in computer graphics and vision,
machine learning, signal processing and many other areas can be
solved by simply expressing the problem as a system of linear
equations and solving using standard techniques.
Linear algebra is defined abstractly in terms of fields, of which
the real and complex numbers are the most familiar examples.
Fields are sets equipped with some notion of addition and multi-
plication as well as negation and reciprocals.
Many discrete mathematical structures commonly encountered
in computer science do not have sensible notions of negation.
Booleans, sets, graphs, regular expressions, imperative programs,
datatypes and various other structures can all be given natural no-
tions of product (interpreted variously as intersection, sequencing
[Copyright notice will appear here once ’preprint’ option is removed.]
or conjunction) and sum (union, choice or disjunction), but gener-
ally lack negation or reciprocals.
Such structures, having addition and multiplication (which dis-
tribute in the usual way) but not in general negation or reciprocals,
are called semirings. Many structures specifying sequential actions
can be thought of as semirings, with multiplication as sequencing
and addition as choice. The distributive law then states, intuitively,
a followed by a choice between b and c is the same as a choice
between a followed by b and a followed by c.
Plain semirings are a very weak structure. We can find many
examples of them in the wild, but unlike fields which provide
the toolbox of linear algebra, there isn’t much we can do with
something knowing only that it is a semiring.
However, we can build some useful tools by introducing the
closed semiring, which is a semiring equipped with an extra opera-
tion called closure. With the intuition of multiplication as sequenc-
ing and addition as choice, closure can be interpreted as iteration.
As we see in the following sections, it is possible to use something
akin to Gaussian elimination on an arbitrary closed semiring, giv-
ing us a means of solving certain “linear” equations over any struc-
ture with suitable notions of sequencing, choice and iteration. First,
though, we need to define the notion of semiring more precisely.
2. Semirings
We define a semiring formally as consisting of a set R, two distin-
guished elements of R named 0 and 1, and two binary operations
+ and ·, satisfying the following relations for any a, b, c 2 R:
a + b = b + a
a +(b + c)=(a + b)+c
a +0=a
a · (b · c)=(a · b) · c
a · 0=0· a =0
a · 1=1· a = a
a · (b + c)=a · b + a · c
(a + b) · c = a · c + b · c
We often write a · b as ab, and a · a · a as a
3
.
Our focus will be on closed semirings [12], which are semir-
ings with an additional operation called closure (denoted
⇤
) which
satisfies the axiom:
a
⇤
=1+a · a
⇤
=1+a
⇤
· a
If we have an affine map x 7! ax + b in some closed semiring,
then x = a
⇤
b is a fixpoint, since a
⇤
b =(aa
⇤
+1)b = a(a
⇤
b)+b.
So, a closed semiring can also be thought of as a semiring where
affine maps have fixpoints.
The definition of a semiring translates neatly to Haskell:
1 2013/7/17
Fun with Semirings
A functional pearl on the abuse of linear algebra
Stephen Dolan
Computer Laboratory, University of Cambridge
stephen.dolan@cl.cam.ac.uk
Abstract
Describing a problem using classical linear algebra is a very well-
known problem-solving technique. If your question can be formu-
lated as a question about real or complex matrices, then the answer
can often be found by standard techniques.
It’s less well-known that very similar techniques still apply
where instead of real or complex numbers we have a closed semir-
ing, which is a structure with some analogue of addition and multi-
plication that need not support subtraction or division.
We define a typeclass in Haskell for describing closed semir-
ings, and implement a few functions for manipulating matrices and
polynomials over them. We then show how these functions can
be used to calculate transitive closures, find shortest or longest
or widest paths in a graph, analyse the data flow of imperative
programs, optimally pack knapsacks, and perform discrete event
simulations, all by just providing an appropriate underlying closed
semiring.
Categories and Subject Descriptors D.1.1 [Programming Tech-
niques]: Applicative (Functional) Programming; G.2.2 [Discrete
Mathematics]: Graph Theory—graph algorithms
Keywords closed semirings; transitive closure; linear systems;
shortest paths
1. Introduction
Linear algebra provides an incredibly powerful problem-solving
toolbox. A great many problems in computer graphics and vision,
machine learning, signal processing and many other areas can be
solved by simply expressing the problem as a system of linear
equations and solving using standard techniques.
Linear algebra is defined abstractly in terms of fields, of which
the real and complex numbers are the most familiar examples.
Fields are sets equipped with some notion of addition and multi-
plication as well as negation and reciprocals.
Many discrete mathematical structures commonly encountered
in computer science do not have sensible notions of negation.
Booleans, sets, graphs, regular expressions, imperative programs,
datatypes and various other structures can all be given natural no-
tions of product (interpreted variously as intersection, sequencing
[Copyright notice will appear here once ’preprint’ option is removed.]
or conjunction) and sum (union, choice or disjunction), but gener-
ally lack negation or reciprocals.
Such structures, having addition and multiplication (which dis-
tribute in the usual way) but not in general negation or reciprocals,
are called semirings. Many structures specifying sequential actions
can be thought of as semirings, with multiplication as sequencing
and addition as choice. The distributive law then states, intuitively,
a followed by a choice between b and c is the same as a choice
between a followed by b and a followed by c.
Plain semirings are a very weak structure. We can find many
examples of them in the wild, but unlike fields which provide
the toolbox of linear algebra, there isn’t much we can do with
something knowing only that it is a semiring.
However, we can build some useful tools by introducing the
closed semiring, which is a semiring equipped with an extra opera-
tion called closure. With the intuition of multiplication as sequenc-
ing and addition as choice, closure can be interpreted as iteration.
As we see in the following sections, it is possible to use something
akin to Gaussian elimination on an arbitrary closed semiring, giv-
ing us a means of solving certain “linear” equations over any struc-
ture with suitable notions of sequencing, choice and iteration. First,
though, we need to define the notion of semiring more precisely.
2. Semirings
We define a semiring formally as consisting of a set R, two distin-
guished elements of R named 0 and 1, and two binary operations
+ and ·, satisfying the following relations for any a, b, c 2 R:
a + b = b + a
a +(b + c)=(a + b)+c
a +0=a
a · (b · c)=(a · b) · c
a · 0=0· a =0
a · 1=1· a = a
a · (b + c)=a · b + a · c
(a + b) · c = a · c + b · c
We often write a · b as ab, and a · a · a as a
3
.
Our focus will be on closed semirings [12], which are semir-
ings with an additional operation called closure (denoted
⇤
) which
satisfies the axiom:
a
⇤
=1+a · a
⇤
=1+a
⇤
· a
If we have an affine map x 7! ax + b in some closed semiring,
then x = a
⇤
b is a fixpoint, since a
⇤
b =(aa
⇤
+1)b = a(a
⇤
b)+b.
So, a closed semiring can also be thought of as a semiring where
affine maps have fixpoints.
The definition of a semiring translates neatly to Haskell:
1 2013/7/17












