PANGOLIN：增量混合模糊测试技术
需积分: 0 192 浏览量
更新于2024-07-01
收藏 1.62MB PDF 举报
"PANGOLIN:增量式混合模糊测试技术通过多面体路径抽象提高效率"
在当前的软件安全测试领域，模糊测试（fuzzing）和符号执行（concolic execution）的混合方法，即混合模糊测试（hybrid fuzzing），已经成为了覆盖率导向的模糊测试技术中的一个重要趋势。这种技术结合了模糊测试的快速覆盖能力和符号执行的精确路径探索，以发现程序中的漏洞和错误。然而，尽管已经有许多研究致力于改进混合模糊测试，现有的非增量式（non-incremental）技术仍然存在效率问题。主要原因是这些技术未能有效利用和重用计算结果，因此错失了许多优化机会。
针对这一问题，研究人员提出了一种名为“多面体路径抽象”（polyhedral path abstraction）的增量式方法。该方法旨在保留符号执行阶段的探索状态，从而在变异和约束求解过程中实现更高效的处理。通过这种方式，与现有的技术相比，可以更有效地进行路径探索，减少重复工作，提高测试效率。
为了实现这一概念，研究团队开发了一个名为PANGOLIN的工具，并使用LAVA-M基准以及九个实际世界的程序进行了评估。评估结果显示，PANGOLIN在发现新路径和触发错误方面表现出色，显著优于传统的非增量式模糊测试工具。这表明，多面体路径抽象策略能够有效地增强模糊测试的性能，特别是在长时间运行的测试场景下，其优势更加明显。
此外，PANGOLIN的创新之处还在于它能够在保持测试覆盖率的同时，减少计算资源的消耗。这对于大规模软件的测试尤其重要，因为这些软件往往需要处理大量的输入和复杂的控制流。通过提供一种更高效、更节省资源的测试手段，PANGOLIN有助于提升软件的安全性和可靠性。
总结来说，PANGOLIN是混合模糊测试领域的最新进展，它的核心是多面体路径抽象技术，能够实现模糊测试和符号执行的增量式集成，从而提高测试效率并发现更多的潜在问题。这一研究成果对于软件开发者和安全专家来说具有重要的参考价值，可以推动未来模糊测试技术的进一步发展。
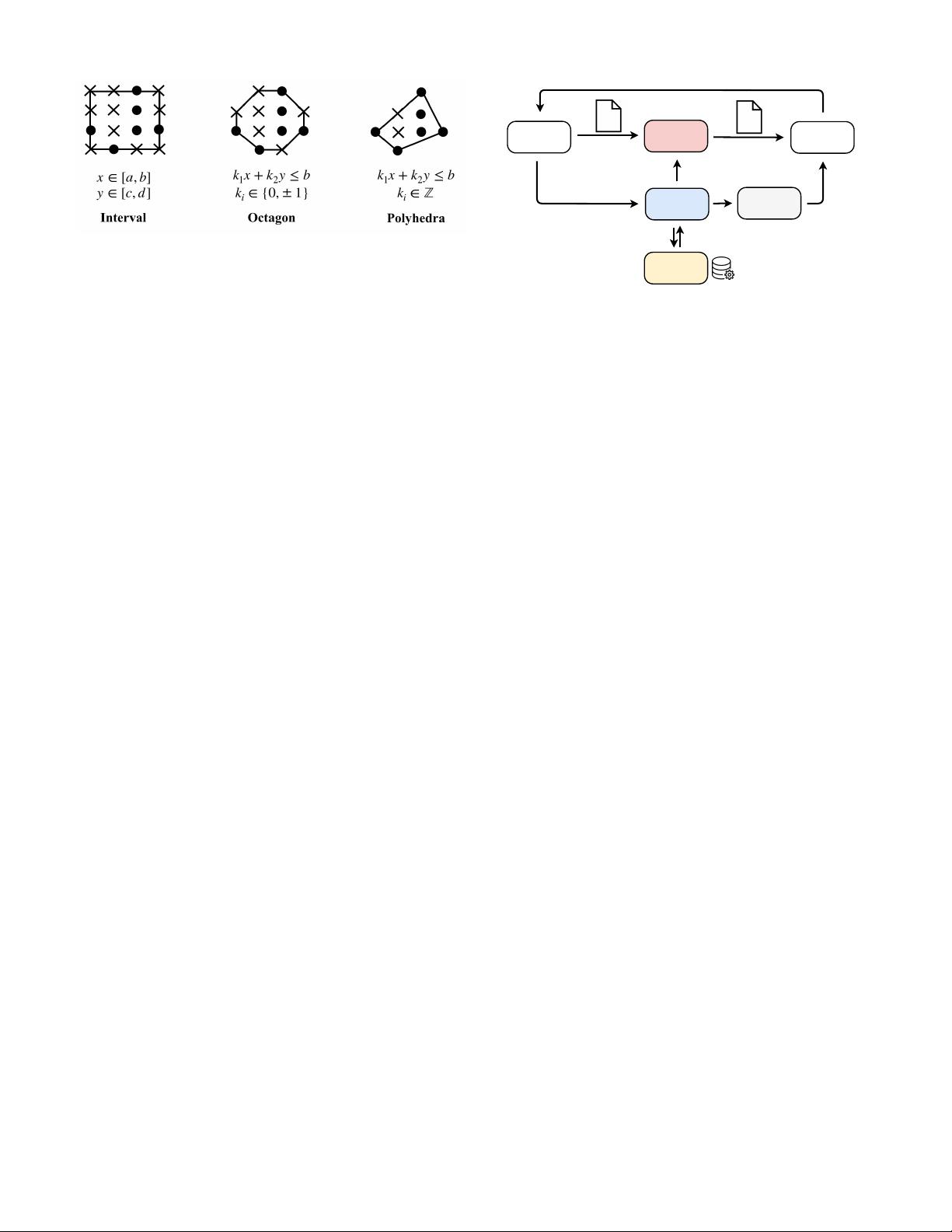
Fig. 2: Different types of path abstraction. In the figure, a, b, c,
and d are constants.
but, unfortunately, still resorts to inefficient mutation to speed
up the exploration of the input space. The lack of effective
guidance to mutation makes their approaches excessively rely
on the heavy-weight constraint solving to achieve a high
coverage rate. First, given a seed input discovered by solving
constraints, randomly mutating it would easily invalidate its
associated path constraints that have already been conquered
by constraint solvers, wasting the computation in exploring
the nearby nested branches. For example, suppose we have
leveraged a solver to obtain a seed input (v = 20, w = 5, x =
3, y = 4, z = 30), which satisfies the predicate at Line 3. Any
new inputs generated by mutating the variables x and y make it
difficult to explore the successive branches at Line 4 and Line
8. Second, with the growth of the nested level of conditional
statements, the path constraints become increasingly restricted,
which makes the mutation less and less efficient. For example,
the predicate (z > 195) at the nested conditional statement of
Line 4 is not difficult to be satisfied by mutation. However,
the path constraint that conjuncts with the predicates at Line
3 and Line 4 (i.e., x = 3 ∧ y = 4 ∧ 195 < z < 200) becomes
challenging for mutation. Even though we already have a seed
input (v = 20, w = 5, x = 3, y = 4, z = 30) and only consider
mutating the variable z, the probability of generating a feasible
input to reach the condition at Line 4 is around 100/2
32
, and
the probability to cover the true-branch of the predicate at Line
4 decreases to 4 /2
32
.
B. Polyhedral Path Abstraction
In this work, we use the notion “path abstraction” to denote
an approximation of a path constraint. In the existing litera-
ture, many different abstractions have been studied, such as
interval [32], octagon [33], and polyhedral [34]. As illustrated
in Figure 2, the interval abstraction only contains the value
ranges of each variable. The octagon abstraction is in the form
k
1
x + k
2
y ≤ b, where x and y are the variables in the path
constraints and k
i
∈ {0, ±1}. The polyhedral abstraction is in
a more general form where k
i
∈ Z. In Figure 2, the black dots
represent all feasible values satisfying a given path constraint,
whereas the crosses represent the infeasible ones. The path
abstraction is the region bounded by the lines representing
multiple linear inequalities.
All the path abstractions approximate non-linear formula in
the given path constraints. All these abstractions are sound,
Executing
Tracing
Seeds
Prioritation
Guided
Constraint
Solving
Seed
Input
Abstraction
Inference
Constrained
Mutation
Abstraction
Reusing
Fig. 3: Architecture of PANGOLIN
because the regions cover all the black dots. However, they
have different levels of the precision. According to the recent
studies [35], [36], the polyhedral abstraction has the best
precision. The example in the Figure 2 also demonstrates the
best performance of the polyhedral abstraction, as only two
infeasible values are confused by the polyhedron.
We further present the properties of the path abstraction
required by a fuzzer and detail how to convert a path constraint
into a polyhedral path abstraction in Section IV-A.
III. OVERVIEW
In this section, we describe the design philosophy of re-
alizing PANGOLIN and illustrate the workflow of PANGOLIN
shown in Figure 3. PANGOLIN is essentially a hybrid fuzzing
technique. It shares the typical components as the conventional
hybrid fuzzing techniques that have been briefly introduced in
Section II, such as seeds prioritization and tracing. We focus
on our discussion on the following ideas.
A. Path Abstraction Inference
We first identify the uncovered branches in fuzzing and
deliver them to the concolic execution engine to proceed.
Different from the concolic execution in the conventional
hybrid fuzzing which invokes the constraint solver to directly
obtain a feasible solution, PANGOLIN constructs a summary of
these uncovered branches, which we denote as the polyhedral
path abstraction. The polyhedral path abstraction describes
a sound search space of the feasible inputs with respect to
the path constraints, which is used to guide the mutation of
the seeds and speed up the solving of the subsequent path
constraints. We explain how to construct a polyhedral path
abstraction in Section IV-A.
B. Constrained Mutation
As the polyhedral path abstraction renders a bounded range
of the input variables with respect to the path constraint of a
path prefix, by sampling from such bounded search space, we
are able to quickly generate a large number of new inputs that
still satisfy this path constraint and, meanwhile, to explore the
subsequent paths sharing the same path prefix. Specifically,
in this work, we adapt an existing sampling technique, the
Dikin walk algorithm [15], to generate new inputs (See Section
剩余14页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2021-04-04 上传
2021-05-20 上传
2021-05-23 上传
2021-02-21 上传
2021-09-29 上传
2022-08-03 上传
