利用演算法与MATLAB计算函数极值

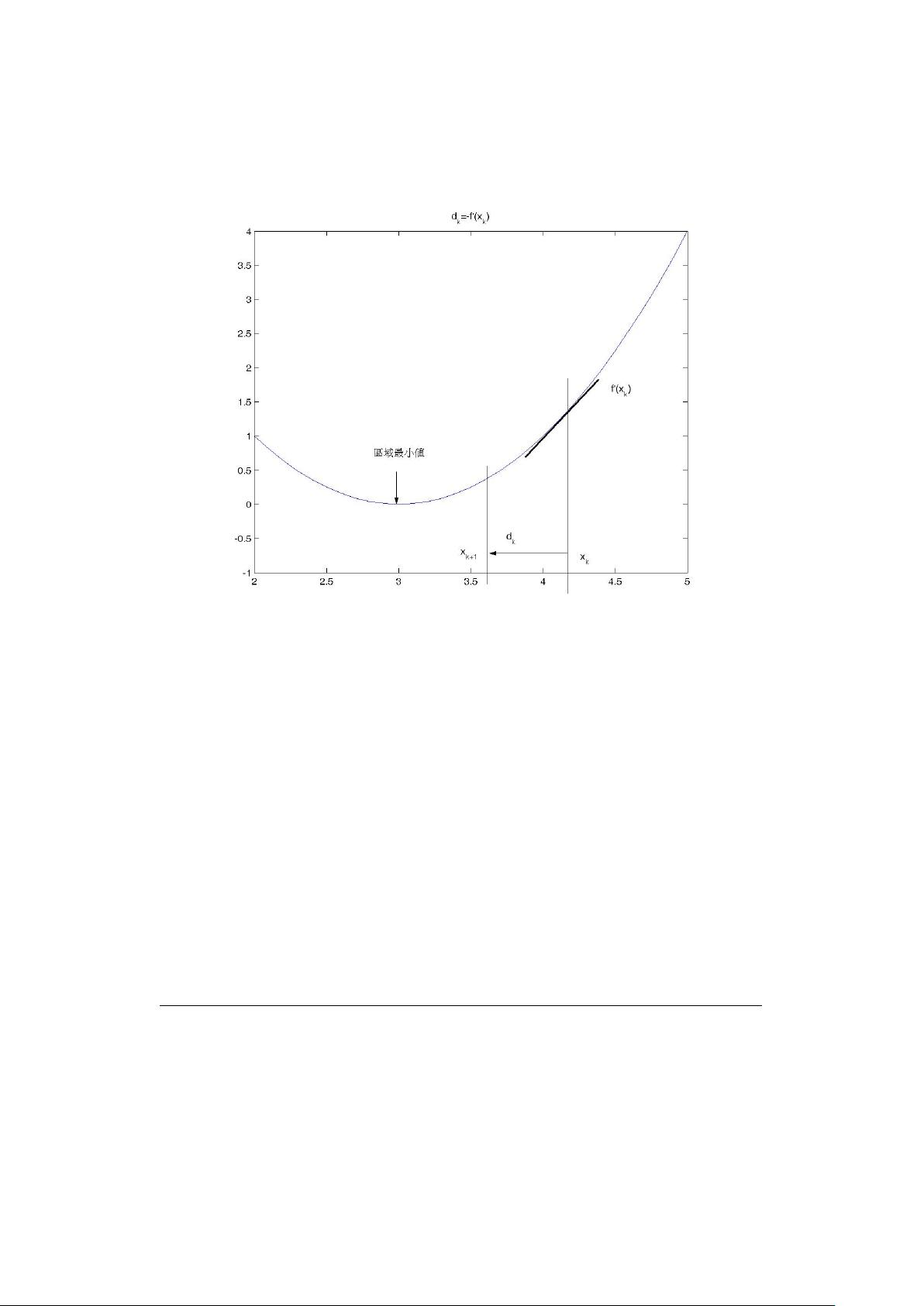
"计算函数极值" 在数学和工程领域，计算函数的极值是一个至关重要的问题，这涉及到寻找函数的最大值或最小值。这在优化问题、统计学中的最大似然估计以及各种科学和工程应用中都有广泛的应用。在处理简单函数时，我们通常会通过求导数来找到极值点，因为这些点对应于导数为零的点。然而，对于复杂或不可导的函数，数值方法变得必不可少。 在MATLAB中，我们可以利用各种工具和函数来实现这一目标。例如，`polyder`函数用于计算多项式函数的导数，`roots`函数则用于找到导数为零的根，即可能的极值点。对于连续但不易解析求导的函数，`fminbnd`可以用来寻找函数在一指定区间的最小值。`inline`函数允许我们将函数定义为内联表达式，便于在代码中使用。此外，`linspace`用于创建等差数列，帮助我们在指定范围内生成测试点，而`num2str`则将数值转换为字符串，方便输出和可视化。 在实际操作中，我们首先会对函数进行分析，比如给定的函数`f(x)=x^4 - 8x^3 + 16x^2 - 2x + 8`，它包含局部最大值和最小值，以及全局最小值。为了找到这些极值，我们首先要计算其一阶导数，然后找出导数为零的点。通过图解，我们可以直观地看到这些点在函数图形上的位置。二阶导数可以帮助我们区分局部极值的性质：若二阶导数在某点为正，则该点是局部最小值；若为负，则是局部最大值。 然而，对于更复杂的函数，我们可能无法轻易地找到解析解，这时就需要借助数值方法。MATLAB中的`fminbnd`函数就是一个例子，它采用了一种叫做黄金分割搜索或边界优化的方法，能够在指定区间内寻找函数的最小值。此外，还可以使用梯度下降法、牛顿法或拟牛顿法等优化算法，这些算法通过迭代逐步接近极值点。 在编写程序时，我们需要考虑如何有效地实现这些算法，并处理可能遇到的问题，如迭代过程中的精度控制、收敛性判断和避免陷入局部最优。编程过程中，学会使用循环结构、条件语句和异常处理是关键。例如，当使用循环寻找极值点时，可能会用到中断循环的技巧，例如在达到预设的迭代次数或满足特定精度条件时停止。同时，匿名函数（lambda函数）的运用可以使代码更加简洁和模块化。 计算函数极值不仅是数学中的基础概念，也是实际问题解决的重要工具。通过MATLAB等软件，我们可以高效地处理复杂函数的极值问题，尽管这可能牺牲了一些精确性，但在实际应用中往往足以提供有价值的解决方案。掌握这些技术和方法，对于解决各种科学和工程问题具有深远的意义。