Python实现线性模型及其应用

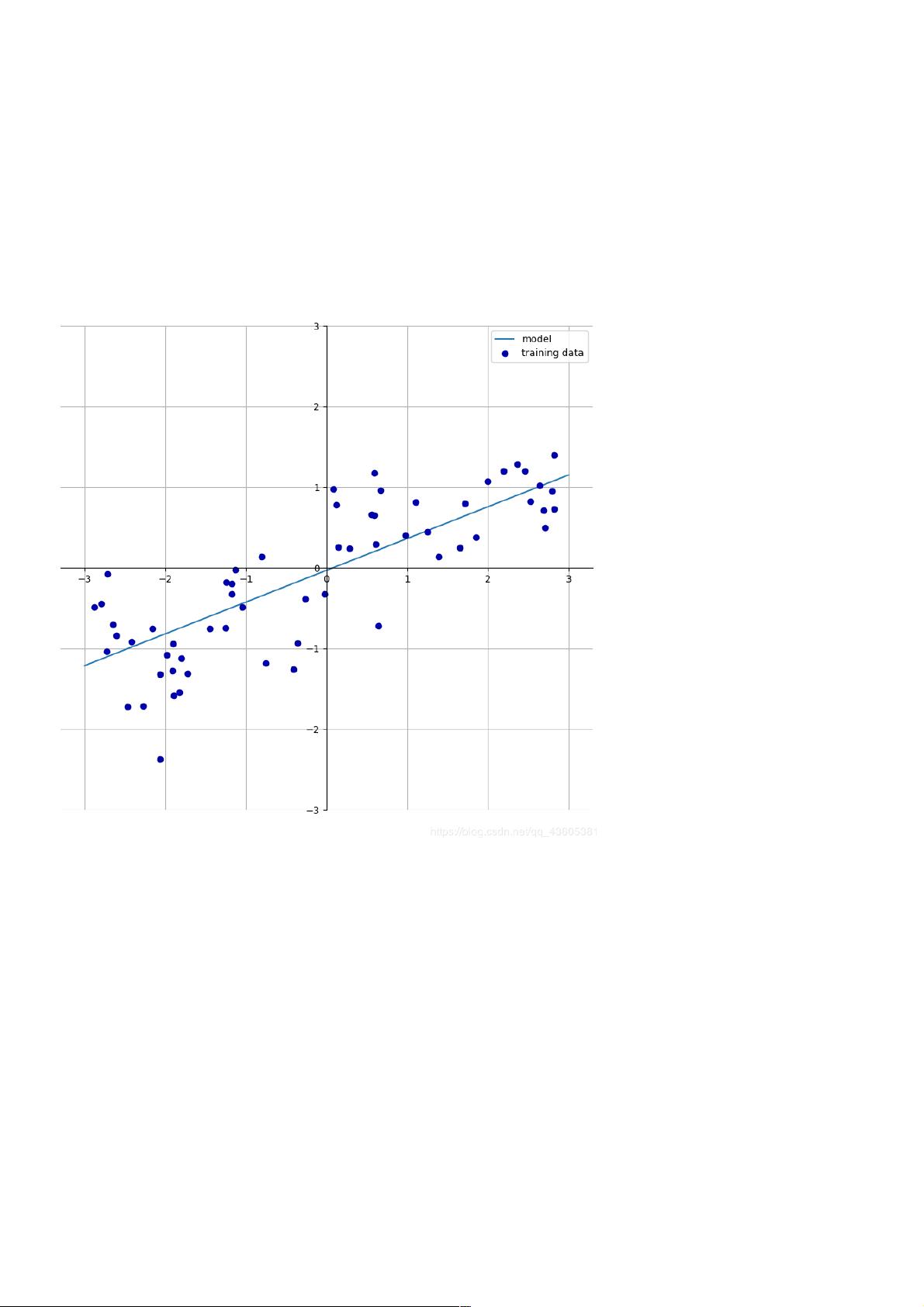
在"Day4_线性模型python实现"这篇文章中，主要探讨的是线性模型在Python中的应用和实践。首先，文章回顾了线性模型的基本概念，特别是回归问题中的线性预测公式，即通过一组特征$x_0, x_1, \ldots, x_p$来预测目标变量$y$，模型形式为$y^ = w_0x_0 + w_1x_1 + \ldots + w_px_p + b$，其中$w_i$是权重参数，$b$是偏置项，$y^$是预测结果。 文章强调了参数学习的过程，如$w$和$b$是通过训练数据拟合得到的，它们的值决定了模型的复杂度。在处理单一特征的数据集时，简化后的公式为$y^ = w_0x_0 + b$。此外，作者还提到了一个实例，展示了如何使用`mglearn`库中的`plot_linear_regression_wave()`函数可视化线性回归模型，以及如何通过`sklearn`库中的`LinearRegression`类来进行线性回归模型的训练和预测。 线性回归，作为最基础的回归算法之一，其目标是找到一组参数使预测值与真实值之间的均方误差最小。均方误差(MSE)衡量了预测值与实际值之间差异的平方和的平均值。尽管线性回归模型简单且直观，但它没有内置的正则化机制，这意味着模型可能会过度拟合训练数据，特别是在特征较多或数据存在噪声时。 文章随后演示了如何使用`train_test_split`函数进行数据划分，并通过`LinearRegression().fit()`对训练数据进行拟合，输出模型的权重参数`lr.coef_`。这部分内容涵盖了模型训练、评估和参数解读的基本步骤。 总结来说，本文通过实际代码展示了如何用Python实现线性回归模型，包括模型的预测公式、参数估计、模型训练和性能评估，这对于理解线性模型的实践应用具有重要的指导意义。同时，它也提醒读者注意线性模型的局限性和可能遇到的问题，如过度拟合，这在选择和调整模型时是不可忽视的。