K均值聚类算法详解：基本与改进版本

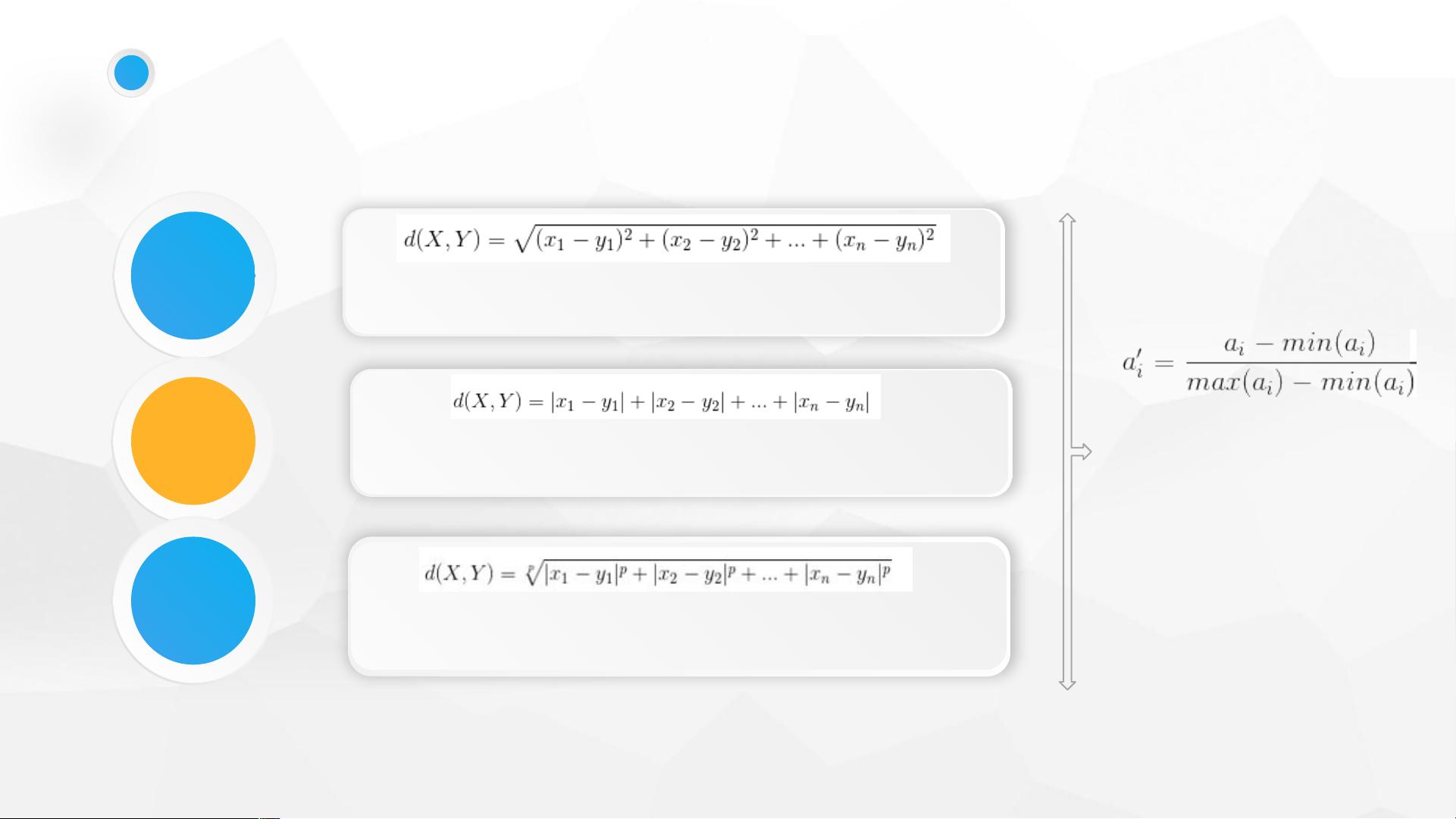
K均值聚类算法是一种常用的无监督机器学习方法，用于数据集的分群，目的是将数据划分为k个互不重叠的簇，每个簇内的数据点彼此相似度高，而不同簇之间的相似度低。该算法的基本思想是迭代地将数据点分配到最近的质心（簇中心），并更新这些质心的位置，直到聚类中心不再改变或达到预设的迭代次数。 PPT内容覆盖了以下几个关键部分： 1. **算法介绍**： - 定义：聚类问题的目标是将元素集合划分为k个簇，每个簇内部差异小，簇间差异大。 - **距离度量**： - 欧几里得距离：固定直角坐标系中两点间的直线距离。 - 闵可夫斯基距离：欧几里得距离和曼哈顿距离的推广，适用于多维空间。 - 归一化处理：确保所有数据在比较时具有相同的尺度。 - **相异度计算**： - 序数变量和分类变量的处理方式不同，前者通过秩值表示，后者通过属性差异率来衡量。 2. **算法流程**： - 初始化：随机选择k个质心，或者使用改进算法如K-means++来初始化。 - 分配：将每个数据点分配到与其最近的质心所在的簇。 - 更新质心：计算每个簇的新质心，作为簇中心。 - 重复步骤2和3，直到簇中心不再改变或达到预设迭代次数。 3. **改进算法**： - K-means++：一种有效的初始化策略，减少初始聚类中心的选择偏差。 - Isodate算法：可能是针对特定场景的优化版本，未详述。 - 二分K均值：将数据集二分处理，降低计算复杂度，适用于大规模数据集。 4. **应用示例**： - 非人恶意流量识别 - 求职信息优化 - 生物种群分析 - 网站关键词和流量分析 - 保险投保者分组 - 用户画像建立 - 商业选址决策 5. **算法限制**： - 对于数据分布、簇的形状和大小敏感 - 需要预先设定簇的数量K - 受初始聚类中心的影响，可能得到局部最优解 - 不适合处理非凸形状的簇和大小悬殊的簇 K-means算法因其简单高效，在大数据处理中表现出色，但对于某些特定条件下的聚类效果可能不尽人意。在实际应用中，可能需要结合其他聚类算法或方法进行调整和优化。