深度学习WGAN解析：稳定性与Wasserstein距离

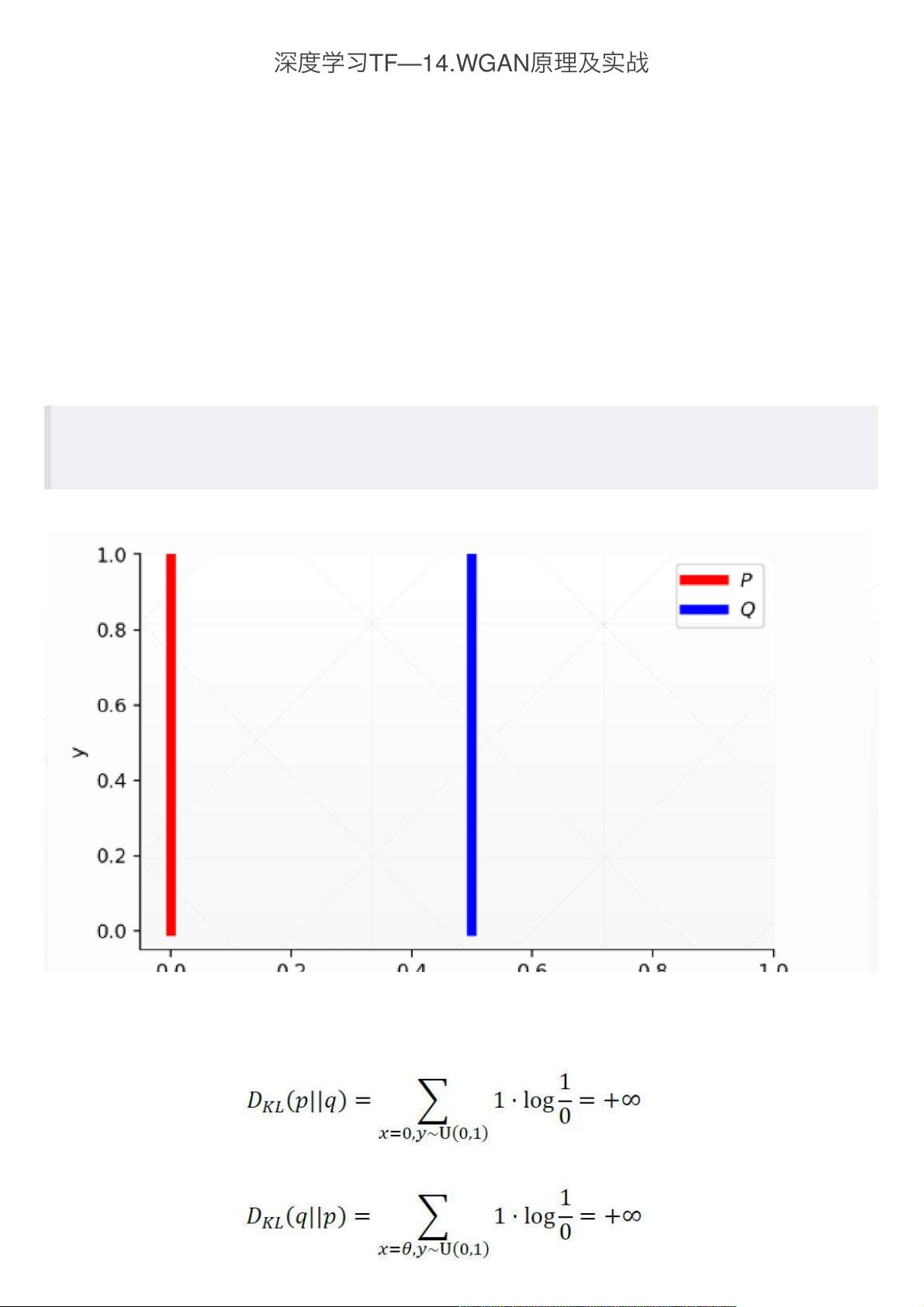
"该资源是关于深度学习中 Wasserstein GAN (WGAN) 的理论与实战的教程。文章深入探讨了为什么传统的 Generative Adversarial Networks (GANs) 在训练过程中可能会遇到不稳定的问题，主要归因于 Jensen-Shannon 散度的局限性，并介绍了 WGAN 如何通过引入 Wasserstein 距离来改善这一状况。" 深度学习领域中的Wasserstein GAN（WGAN）是一种改良版的生成对抗网络，旨在解决原始GAN在训练过程中可能遇到的不稳定性问题。这篇文档详细阐述了WGAN的基本原理和实际应用，帮助读者理解其背后的数学概念。 首先，文档指出GAN训练不稳定的根源在于Jensen-Shannon (JS) 散度。JS散度是一种衡量两个概率分布差异的指标，但在分布不重叠的情况下，它的梯度为零，这导致了GAN在训练过程中的梯度消失问题，使得网络无法有效收敛。为了解决这个问题，WGAN引入了Wasserstein距离，也称为Earth Mover's（EM）距离。 Wasserstein距离提供了一种衡量两个概率分布之间“距离”的新方法。它定义为从一个分布到另一个分布的最小子距离代价，即所有可能联合分布的期望最小值。这种距离考虑了分布之间的实际几何差异，即使分布不重叠也能提供有意义的梯度信息，从而改进了训练过程的稳定性和效率。 通过比较JS散度和Wasserstein距离的曲线，文档进一步说明Wasserstein距离如何更平滑地反映分布之间的变化，尤其是在分布不重叠时，可以提供连续的梯度，有利于网络参数的更新。因此，WGAN的优化目标是减小生成器产生的样本分布与真实数据分布之间的Wasserstein距离，从而提高生成样本的质量。 在实战部分，文档可能涵盖了如何设置和训练WGAN模型，包括权重clipping等技术，这些技术用于确保Wasserstein距离的线性可微性，以及如何在具体的数据集上应用WGAN进行图像生成或其他任务。通过这种方式，读者不仅能理解WGAN的理论，还能掌握如何在实际项目中运用这些概念。 这篇资源对于想要深入理解和应用WGAN的深度学习从业者来说是一份宝贵的资料，它提供了理论基础和实践指导，有助于提升对生成模型稳定训练的理解和技能。