科罗拉多河域水电优化分配：遗传算法与多目标模型

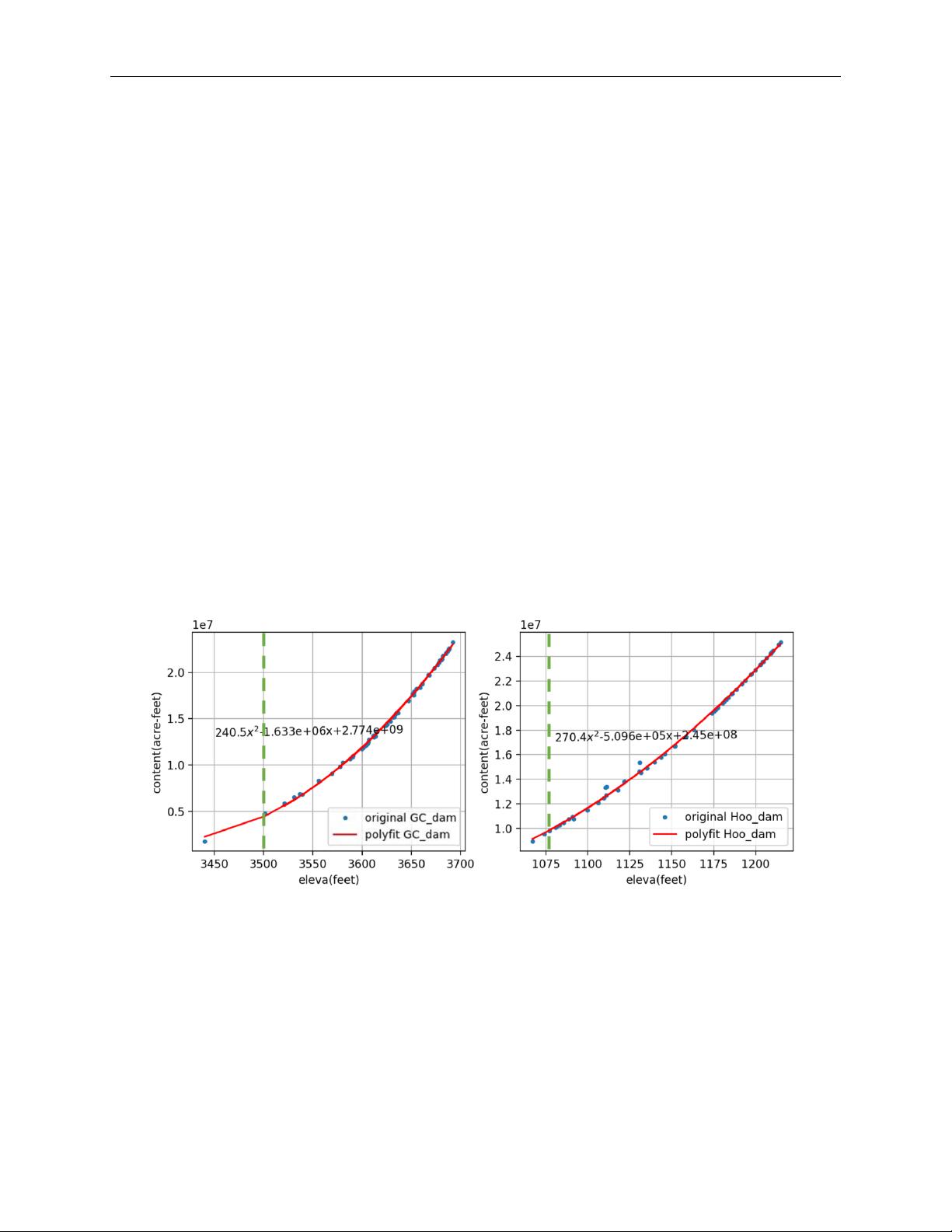
"2022年美国数学建模竞赛（MCM）的F题——‘水电共享’，团队通过建立多目标优化模型、AHP（层次分析法）和TOPSIS（技术、运营和综合选择法）组合评估模型以及单目标线性规划模型，解决科罗拉多河流域在水资源短缺情况下的水电分配问题。" 本文主要围绕科罗拉多河流域的水电资源分配挑战展开，旨在制定一个合理且可辩护的水分配策略。团队首先收集了关于科罗拉多河流域的详细水文数据，包括五个州的人口、工业产出、农业产量、GDP以及电力需求等信息，通过数据可视化方法使结果更直观。 **多目标优化模型（Model I）**： 为了平衡社会目标和经济目标，团队构建了一个具有四个目标的多目标优化模型。模型考虑了水与电对于社会福祉和经济发展的重要性，重点在于如何协调两个水坝的工作，以实现水资源的最大效益。这一模型可能涉及到水资源的经济效益、生态环境保护、社会福利等多个层面的均衡。 **AHP和TOPSIS组合评估模型（Model II）**： 层次分析法（AHP）用于确定不同因素之间的相对权重，帮助决策者在多个相互竞争的标准之间进行权衡。而TOPSIS方法则通过计算每个方案与理想解和负理想解的距离，对各种分配策略进行排序和选择，以找到最接近理想解的解决方案。这两种方法结合使用，可以更全面地分析和量化公平性系数，为水资源分配的公平性提供依据。 **单目标线性规划模型（Model III）**： 相对于多目标优化的复杂性，单目标线性规划模型可能更侧重于解决特定的优化问题，如最小化成本或最大化产出。在这个问题中，可能是为了找出在满足特定约束条件下，如何有效地分配水资源以满足各州的需求。 团队通过这些模型的建立和应用，不仅解决了水资源的分配问题，还为应对科罗拉多河流域的干旱和高温挑战提供了策略建议。他们的研究方法和成果对于水资源管理领域具有重要的理论和实践价值，能够为类似的区域水资源分配问题提供参考。