Architecting the Discontinuous Deformation Analysis Method Pipeline on the GPU
Yunfan Xiao, Min Huang, Qinghai Miao*, Jun Xiao and Ying Wang
School of Engineering Science
University of Chinese Academy of Science
Beijing, China
E-mail: xiaoyunfan12@mails.ucas.ac.cn {huangm, miaoqh, xiaojun, ywang}@ucas.ac.cn
Abstract—As an important numerical analysis method of
rock mechanics, discontinuous deformation analysis (DDA)
has been widely used in rock engineering. DDA has certain
advantages such as the large time step and the large
deformation, at the cost of relatively low computing
efficiency. To address the efficiency bottleneck of DDA, this
paper proposes a complete graphics processing unit (GPU)-
based version. The entire DDA pipeline, involving contact
detection, global matrix building, linear equation solving,
and interpenetration checking, is restructured according to
the GPU architecture to minimize data transmissions
between the host and device. For the equation solver in
DDA, a comparison study of the conjugate gradient method
with different preconditioners, i.e., block Jacobi, symmetric
successive over-relaxation (SSOR) approximate inverse, and
ILU, is introduced first, and a novel sparse matrix-vector
multiplication (SpMV) method, intended for the sparse
block symmetry matrix with distinct features and which
outperforms cuSPARSE by 2.8 times, is proposed as well.
Schemes to solve memory write conflicts and branch
divergences on the GPU are also introduced in contact
detection, global matrix building, and interpenetration
checking. For the stable analysis of a slope, the proposed
GPU-based DDA with double precision achieved a speed-up
rate that was 48.72 times higher than that of the original
CPU-based serial implementation.
Keywords-Discontinuous Deformation Analysis, Graphics
Processing Unit (GPU), Sparse Matrix-vector Multiplication
(SpMV), Contact Detection, Memory Write Conflict, Branch
Divergence
I. INTRODUCTION
Discontinuous deformation analysis (DDA) is a type of
discrete element method originally proposed by Shi in
1988. It can analyze the mechanical response of blocky
systems under general loading and boundary conditions.
Large displacements and deformations are considered
under both static and dynamic loadings [1].
DDA simulates the interaction of discrete bodies with
multi-time steps as discrete element method (DEM), but
solves stress-displacement problems in each step as finite
element method (FEM). DDA derives the global
simultaneous equations from the minimum potential
energy principle and takes displacements as unknowns,
which are solved in each iterative step. On the other hand,
DDA gives a real dynamic solution with the correct energy
consumption by frictional resistance at contact and at the
velocities passing between the successive steps [2].
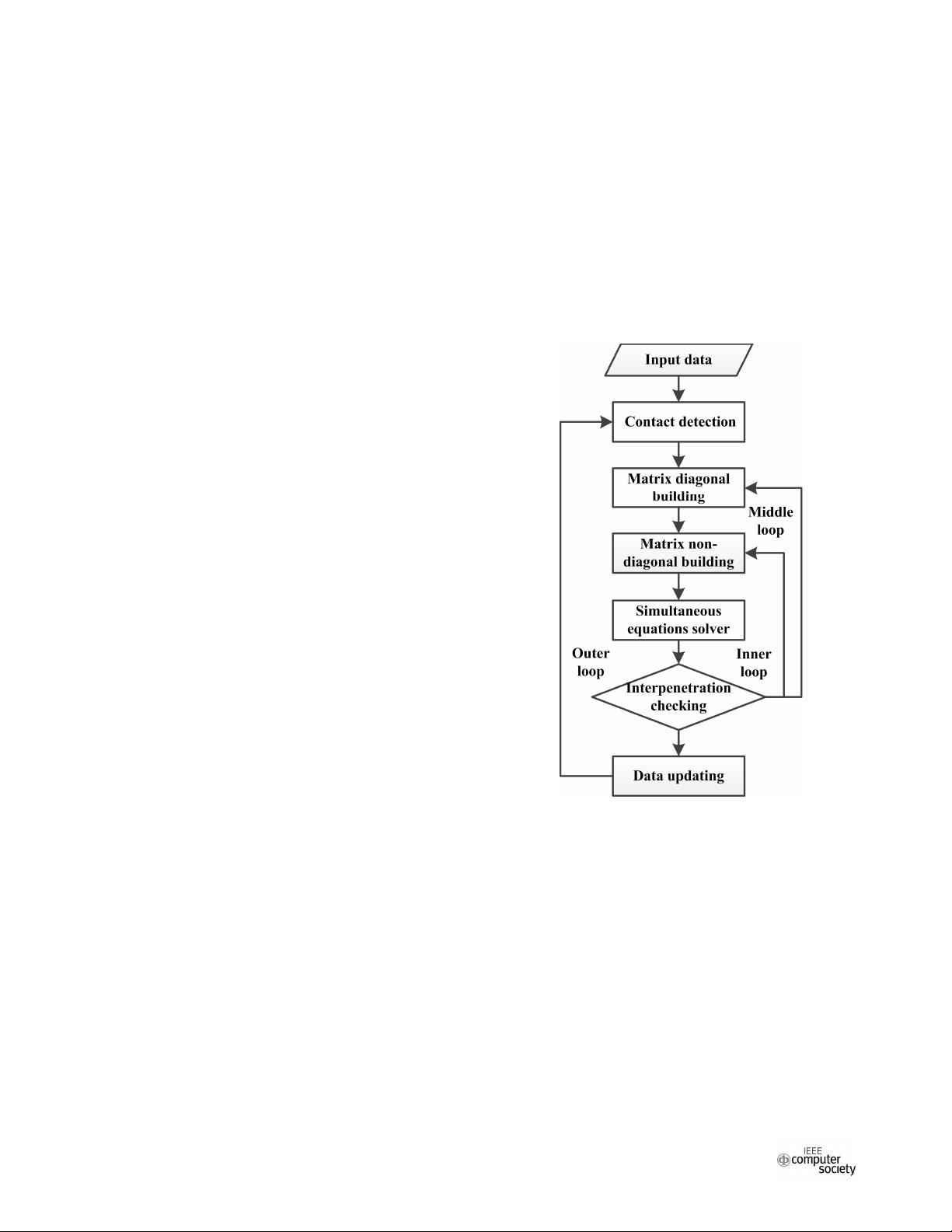
Figure 1. The pipeline of DDA on the CPU
These advantages of DDA lead to massive
computation. Besides data input, the pipeline of DDA
mainly includes six computing modules, including the
contact detection module, global stiffness matrix diagonal
building module, global stiffness matrix non-diagonal
building module, sparse linear symmetry equation solving
module, interpenetration checking module, and data
updating module. As illustrated in Fig. 1, the iterative loop
in the pipeline has three nested loops. The outer loop (loop
1) is the multi-time iterative step. The results of the
previous step will be the input data of the next step. This
iterative step allows DDA to simulate the large
displacement and deformation in blocky systems. The
middle loop (loop 2) is the maximum allowed
displacement iterative process. The displacement of each
block in the current step must be less than the double of
the maximum allowed displacement, which is a control
2017 IEEE International Parallel and Distributed Processing Symposium Workshops
978-0-7695-6149-3/17 $31.00 © 2017 IEEE
DOI 10.1109/IPDPSW.2017.93
1188
2017 IEEE International Parallel and Distributed Processing Symposium Workshops
978-1-5386-3408-0/17 $31.00 © 2017 IEEE
DOI 10.1109/IPDPSW.2017.93
1188









