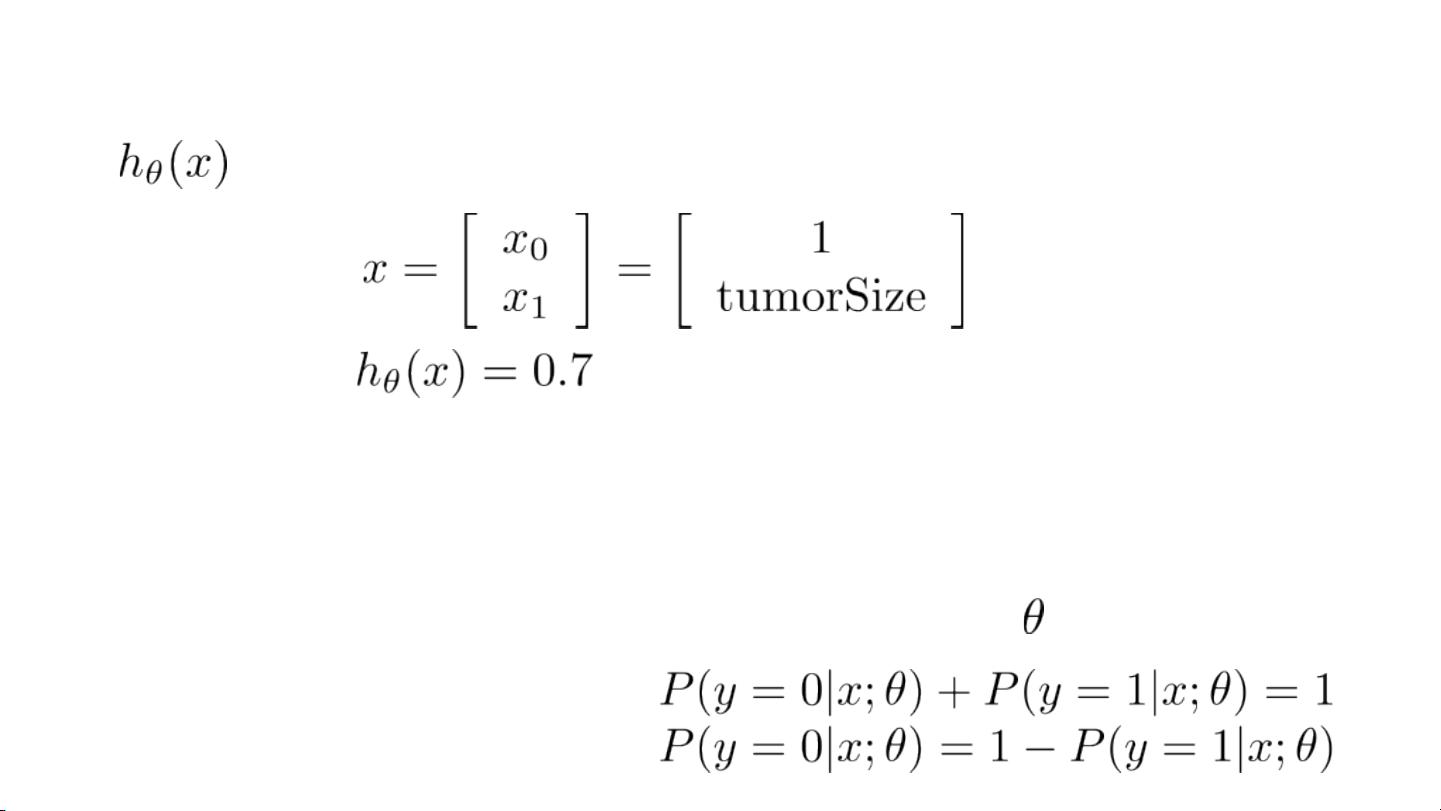斯坦福大学机器学习课：逻辑回归与分类

"2014斯坦福大学机器学习课程，第六讲：逻辑回归 Logistic Regression" 在机器学习领域，逻辑回归（Logistic Regression）是一种广泛应用于分类问题的算法，尤其适用于二分类问题。在这个PPT中，它被用作示例来解决如电子邮件分类（垃圾邮件/非垃圾邮件）、在线交易欺诈检测（是/否）以及肿瘤诊断（恶性/良性）等实际问题。 1. **二分类问题**： - 在这些例子中，我们关注的是两个可能的结果，例如邮件是否为垃圾邮件，交易是否为欺诈，或者肿瘤是否恶性。对于二分类问题，我们通常定义一个输出变量y，取值为0或1，分别代表“负类”（例如良性肿瘤）和“正类”（例如恶性肿瘤）。 2. **逻辑回归假设表示**： - 逻辑回归的假设函数（hypothesis function）通过sigmoid函数（也称为逻辑函数）来实现，该函数将线性函数的输出映射到0到1之间，提供了一个概率估计。对于输入x，假设函数hθ(x)表示y=1的概率。 3. **决策边界**： - 逻辑回归可以创建一个决策边界，用于区分不同的类别。如果hθ(x)大于某个阈值，我们预测y=1，反之则预测y=0。这个边界可以是线性的，也可以是非线性的，取决于特征空间的复杂性。 4. **非凸成本函数**： - 在线性回归中，成本函数通常是凸的，意味着存在唯一最小值。然而，在逻辑回归中，原始的成本函数是“非凸”的，这可能导致在训练过程中陷入局部最小值。因此，我们使用一个简化版的成本函数，以确保其在优化时是凸的，这样就能保证找到全局最小值。 5. **梯度下降法**： - 为了最小化逻辑回归的成本函数，通常采用梯度下降法。在逻辑回归的简化成本函数和梯度下降的框架下，我们可以有效地更新模型参数θ，从而逐步优化模型的性能。 6. **训练集与成本函数**： - 训练集包含m个例子，每个例子都有对应的已知标签y。逻辑回归的成本函数是基于所有训练样本计算的，它综合了所有样本的错误率，以评估模型的性能并指导参数的调整。 逻辑回归的实用性和灵活性使其在许多现实世界的问题中表现出色，尤其是在预测事件发生的可能性时。通过理解这些基本概念，我们可以更好地利用这个强大的工具来解决实际的分类挑战。