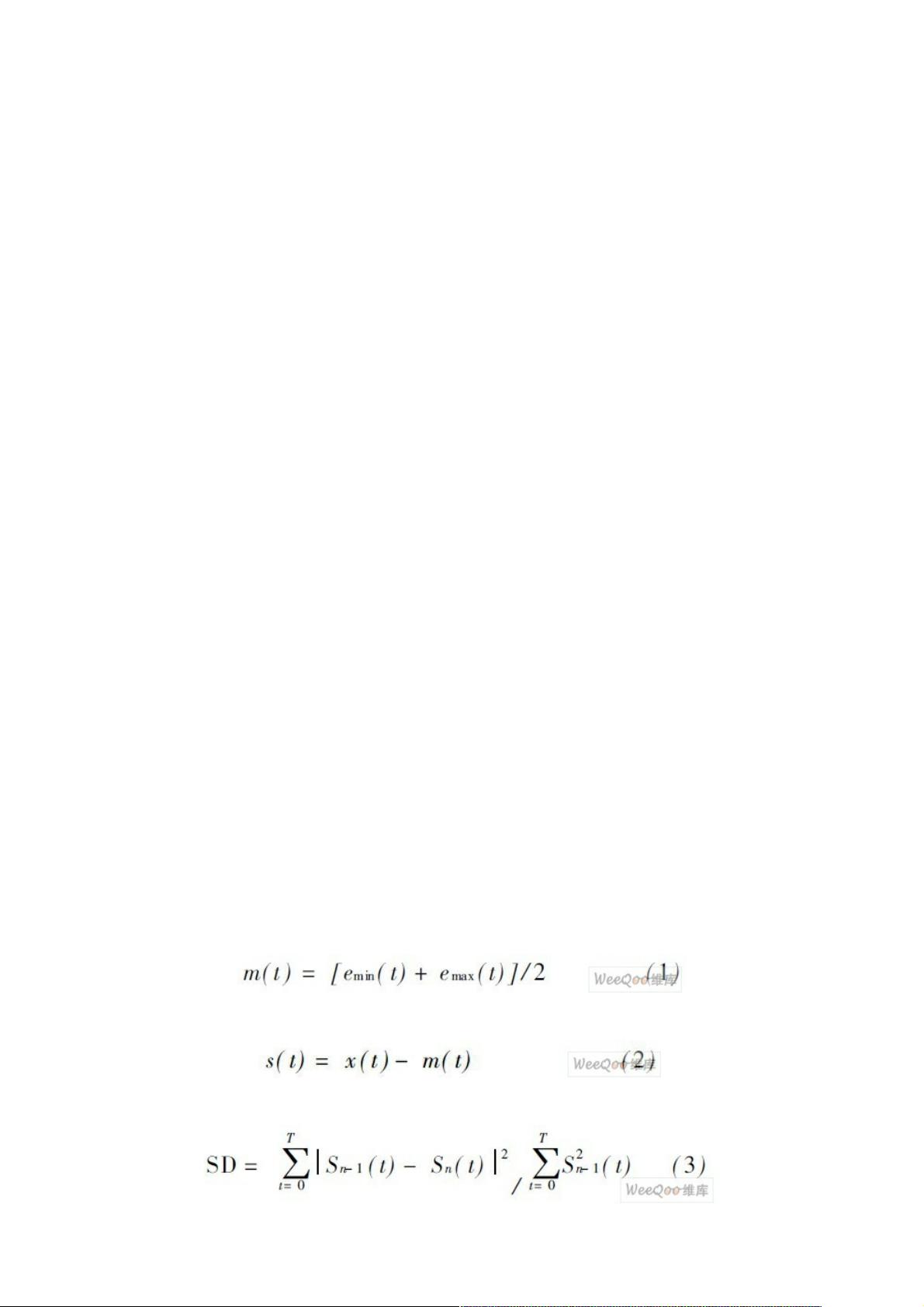EEMD在信号处理中的应用与改进：从HHT到EEMD

"本文主要探讨了基于EEMD(Ensemble Empirical Mode Decomposition)的信号处理方法，该方法是对Hilbert-Huang变换（HHT）的一种改进，旨在更有效地分析非线性非平稳信号。HHT由N.E. Huang在1998年提出，它包括经验模式分解(EMD)和希尔伯特变换(Hilbert Transform)两部分，能够在时间和频率域同时提供信号的信息。然而，EMD在处理过程中可能会出现虚假分量和模态混叠问题，EEMD通过添加噪声辅助分析来解决这些问题，提高了分解的准确性和稳定性。 EEMD是一种集合经验模式分解的方法，通过在原始信号中添加白噪声来补充不同时间尺度，从而避免模态混叠。这种方法在Matlab环境中实现，利用GUI界面，便于用户进行比较分析和验证EEMD在抗混叠性能上的优势。 在HHT中，EMD是关键步骤，它将复杂信号分解为一系列内在模态函数(IMFs)。IMFs需满足两个条件：在整个时间序列中，局部极大值和局部极小值的个数最多相差一个，且在任一端点的包络均单调。这些IMFs代表了信号的不同时间尺度成分，每个IMF对应着信号的一个特定频率成分或特征时间尺度。 希尔伯特变换随后应用于这些IMFs，生成瞬时频率和瞬时振幅，提供了信号的时频分布，揭示了信号在时间和频率上的变化。这种方法特别适合于分析非线性、非平稳信号，如生物医学信号、地震数据、经济时间序列等。 然而，EEMD并非没有挑战，它需要正确选择噪声的幅度和处理多次运行的平均问题。此外，虽然EEMD减少了虚假分量，但在某些情况下，仍可能存在过度分解或欠分解的问题，这需要通过调整参数和理解信号特性来优化。 EEMD是一种强大的工具，尤其在处理复杂信号时，它提供了一种自适应和稳健的时频分析手段，克服了传统傅里叶变换和短时傅里叶变换等方法的局限性。然而，使用EEMD进行信号分析时，需要对信号性质有深入理解，并适当调整方法参数，以确保最佳的分解效果。"