PSO工具箱快速入门：优化函数的利器

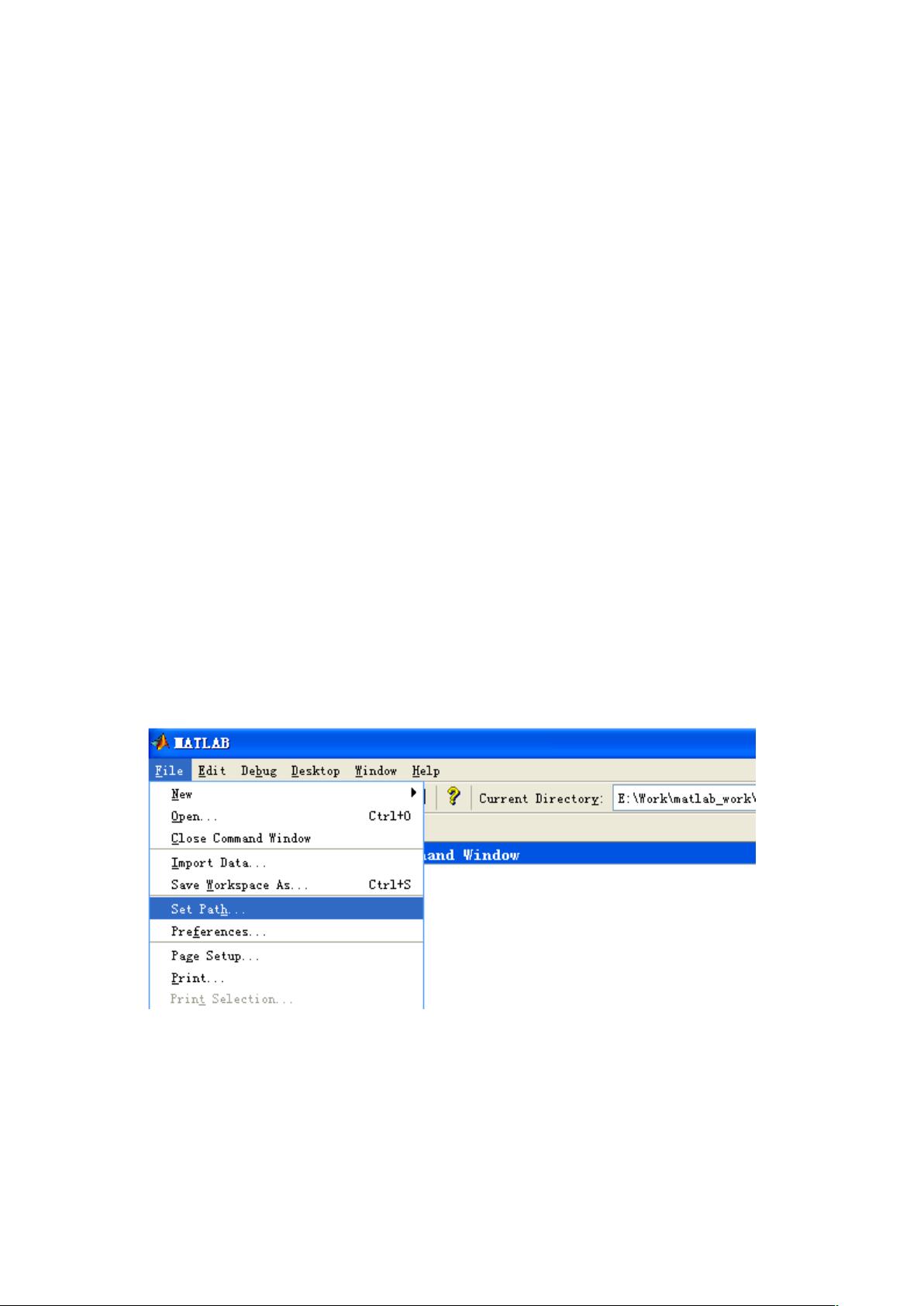
"这篇文档是关于PSO工具箱的使用指南，主要介绍如何利用该工具箱进行粒子群优化算法（PSO）的应用。" 粒子群优化（PSO）是一种基于群体智能的全局优化算法，源自对鸟群飞行行为的模拟。PSOt工具箱将PSO算法的关键部分封装，简化了用户在Matlab环境中使用该算法的过程。用户只需定义目标函数，设置自变量范围和最大速度等参数，即可进行优化。 相比于遗传算法，PSO通常需要调整的参数较少，这使得它在实际应用中更为简便。PSO算法对优化问题的限制较少，无论目标函数是否可微分、连续，都能处理多变量、非线性、不连续的问题，因此在解决复杂优化问题时表现出色。 使用PSOt工具箱的步骤主要包括： 1. **设置工具箱路径**：在Matlab命令窗口通过“File > SetPath…”添加工具箱所在目录，若需要使用测试函数或神经网络训练，还需相应设置其他子目录。 2. **定义目标函数**：根据实际需求编写M文件，例如在`test_func.m`中定义一个需要求最小值的二元函数。例如，对于函数`z=0.5*(x-3)^2+0.2*(y-5)^2-0.1`，其中x和y的范围为[-50,50]，可以创建一个函数来返回该目标值。 3. **调用PSO核心函数**：使用`pso_Trelea_vectorized()`函数执行优化过程。此步骤需要根据优化问题的具体情况设置参数，如种群大小、最大迭代次数、学习因子等，以达到理想的收敛效果。 在进行参数设置时，需要注意以下几点： - **种群大小**（Population Size）：指参与搜索的粒子数量，较大的种群通常能探索更广泛的解决方案空间，但计算量也会增加。 - **最大速度**（Max_V）：限制了粒子在搜索空间中的移动速度，防止过快或过慢的收敛。 - **学习因子**（Learning Factors）：包括个人历史最优（c1）和全局最优（c2），影响粒子更新速度和方向。 - **惯性权重**（Inertia Weight）：控制旧速度对新速度的影响，通常随着迭代进行逐渐减小，以平衡全局和局部搜索。 在优化过程中，PSO算法会不断迭代，粒子的位置和速度会根据当前最优解和全局最优解进行更新。最终，算法将收敛到一个或多个局部或全局最优解。 总结来说，PSOt工具箱提供了一个方便的平台，使得非专业优化算法开发者也能应用PSO解决实际问题。正确理解和配置参数，结合适当的调试，用户能够有效地利用PSO工具箱解决各类复杂的优化任务。