向量基础：描述空间的工具与Python操作

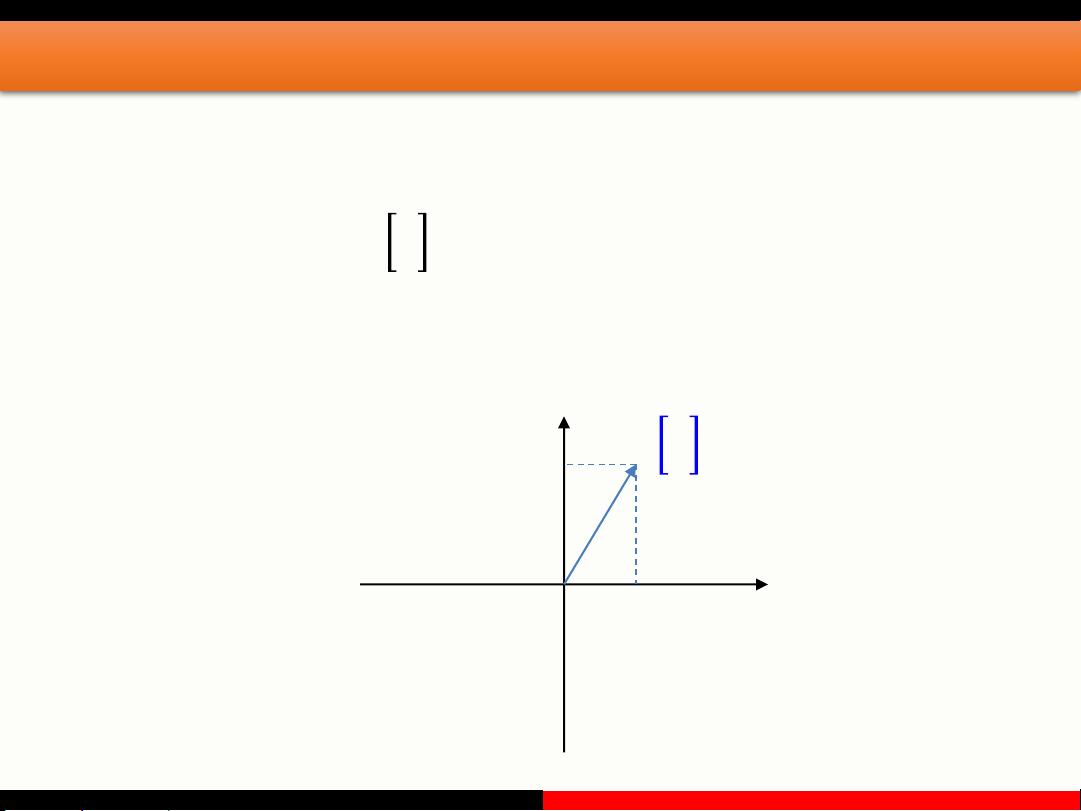
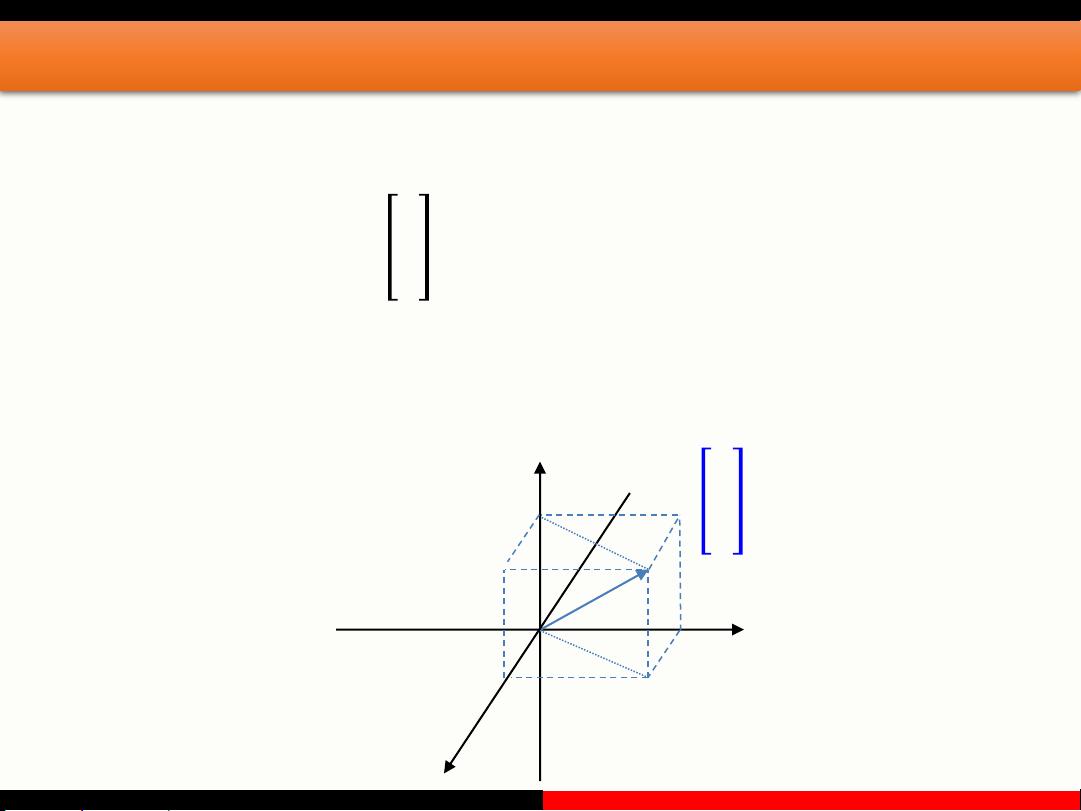
本讲义主要聚焦于计算机数学中的向量基础知识，旨在帮助学习者理解和掌握描述空间的关键工具。在第02讲中，主要内容涵盖了以下几个方面： 1. **向量基本知识回顾**：首先回顾了向量的基本概念，包括其在数学中的正式定义，如欧几里得向量、几何向量或矢量，这些是具有大小（长度）和方向的量，通常通过带箭头的线段来可视化表示。向量可以用印刷体小写粗斜体字母（如a, b, u, v）表示，手写体时会在字母上加箭头，或者用起点（如𝑨）和终点（如𝑩）来标记，也可以在空间直角坐标系中用数对形式（如(2,3)）展示。 2. **列向量与Python描述**：列向量是向量的一种特殊形式，它是一系列数据元素按列排列。这部分内容将介绍如何在Python编程语言中有效地操作和处理向量，可能涉及numpy等库的使用。 3. **向量的范数**：范数是衡量向量大小的重要指标，它定义了向量在空间中的长度或模。理解向量的范数对于计算距离、正则化等数学运算至关重要。 4. **常用向量**：列举了一些在数学和计算机科学中常见的向量类型，如单位向量（长度为1的向量）、零向量（大小为零但方向不确定的向量）等，这些向量在各种算法中扮演着基础角色。 5. **向量的运算**：深入探讨了向量的加法、数乘（标量乘法）以及向量间的乘法（如点积和叉积），这些都是构建向量空间模型的基础运算。 6. **线性组合**：介绍了如何通过线性组合的方式来表达一个向量是另一个向量的线性函数，这是线性代数中一个核心的概念，常用于表示复杂系统中的变化关系。 7. **向量在空间中的应用**：阐述了向量在空间中的重要地位，它作为描述空间结构的工具，被广泛应用于各种计算和分析领域，如机器学习中的特征表示、图像处理中的像素组合、信号处理中的波形分析等。 通过这一系列讲解，学习者将能够建立起扎实的向量理论基础，并能在后续的计算机数学课程和实际项目中灵活运用向量这一关键工具。