八数码难题搜索求解实验报告——广度优先搜索
版权申诉
184 浏览量
更新于2024-07-06
收藏 247KB PDF 举报
"这篇实验报告主要探讨了八数码难题的搜索求解,通过广度优先搜索算法进行演示。实验由信息科学与工程学院自动化0901班的孙锦岗同学完成,指导教师为刘丽珏。实验目的是理解图搜索策略,掌握搜索算法,具体实现八数码难题的搜索过程。报告中提到了八数码难题的规则,即在3x3的棋盘上,通过移动空格来达到目标状态。实验采用的数据结构是队列,利用队列的先进先出特性来保存和扩展节点。算法分析部分指出,由于九宫问题的排列组合数量巨大,采用广度优先搜索可以有效地避免数组记录所有节点排列导致的内存问题。"
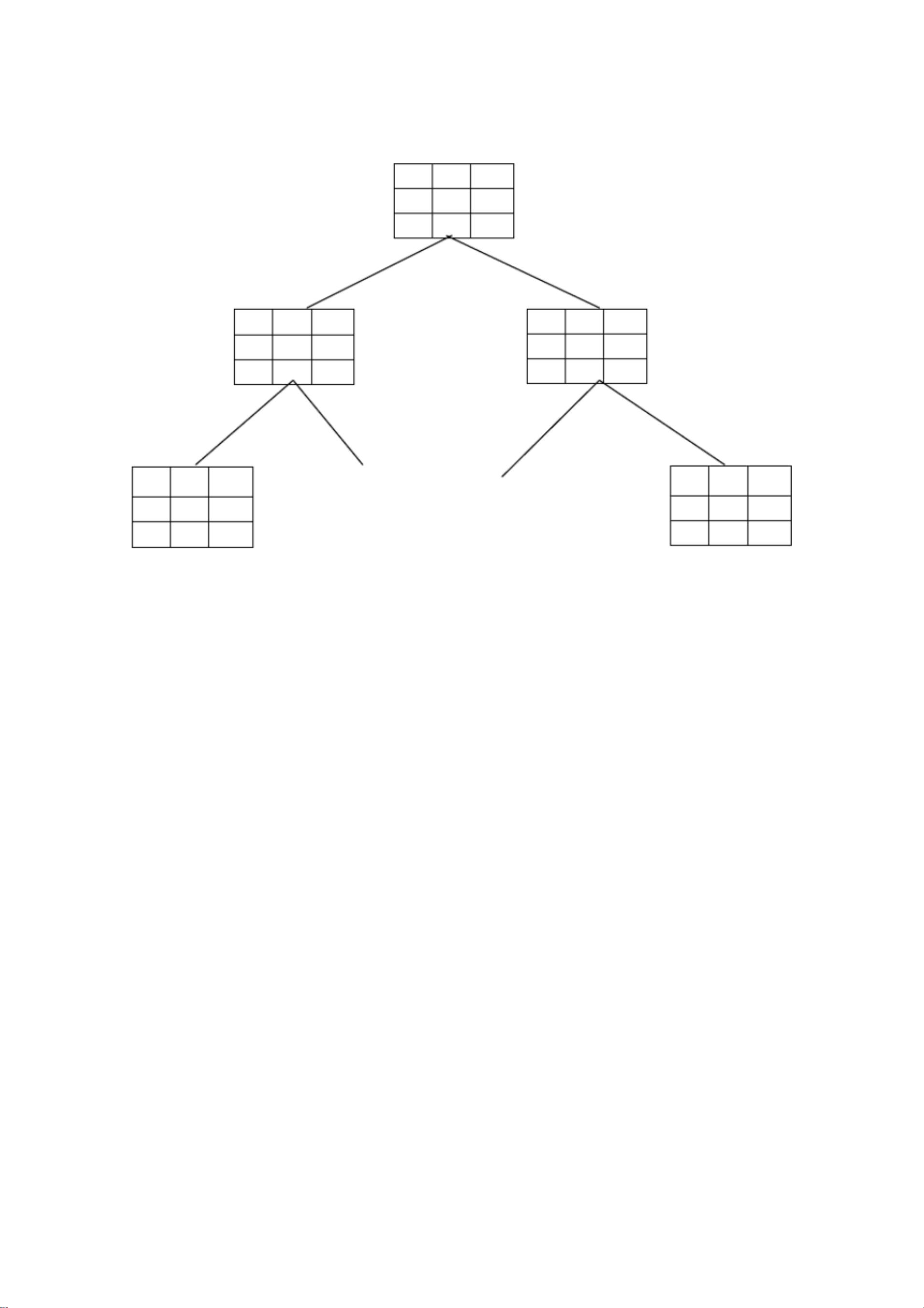
在八数码难题中,每个状态可以用一个3x3的矩阵表示,包含数字1到8以及一个空格(通常用0表示)。初始状态和目标状态是给定的,目标是通过有限次合法移动将初始状态转变为目标状态。合法移动包括将空格上、下、左、右四个方向移动。实验采用的搜索策略是广度优先搜索(BFS),这种策略能保证找到最短的解,因为它总是先探索离起点近的节点。
广度优先搜索的工作原理是使用队列作为数据结构。首先,将初始状态放入队列,然后不断从队列头部取出状态,检查是否为目标状态。如果不是,就生成该状态的所有可能后继状态,并将它们入队,同时记录每个新状态的父节点,以便找到解时可以回溯路径。这个过程会一直持续,直到找到目标状态或队列为空。由于广度优先搜索的特点,它可以避免陷入深度优先搜索可能导致的无限循环或过深的搜索树。
实验中提到的计算奇偶序列解法是另一种解决思路,但报告主要集中在广度优先搜索的实现上。在实际编程实现时,通常会使用哈希表或HashSet来检测重复状态,以避免无效的重复搜索,提高效率。
实验报告的最后提到了九宫问题的全排列数量,即9!,这是一个非常大的数字,表明问题的复杂性。采用广度优先搜索策略可以有效地控制搜索空间,减少所需的计算资源。
总结来说,这份实验报告详细介绍了如何运用广度优先搜索算法解决八数码难题,强调了数据结构的选择(队列)以及搜索过程中避免重复状态的方法,对于理解搜索算法在实际问题中的应用具有很好的示例价值。
2022-11-13 上传
2022-11-13 上传
2018-06-16 上传
2021-10-29 上传
2021-07-03 上传
2021-06-27 上传
2019-08-16 上传
2021-07-17 上传
2021-07-10 上传
lzx13599381087
- 粉丝: 2
- 资源: 9万+
最新资源
- 深入浅出:自定义 Grunt 任务的实践指南
- 网络物理突变工具的多点路径规划实现与分析
- multifeed: 实现多作者间的超核心共享与同步技术
- C++商品交易系统实习项目详细要求
- macOS系统Python模块whl包安装教程
- 掌握fullstackJS:构建React框架与快速开发应用
- React-Purify: 实现React组件纯净方法的工具介绍
- deck.js:构建现代HTML演示的JavaScript库
- nunn:现代C++17实现的机器学习库开源项目
- Python安装包 Acquisition-4.12-cp35-cp35m-win_amd64.whl.zip 使用说明
- Amaranthus-tuberculatus基因组分析脚本集
- Ubuntu 12.04下Realtek RTL8821AE驱动的向后移植指南
- 掌握Jest环境下的最新jsdom功能
- CAGI Toolkit:开源Asterisk PBX的AGI应用开发
- MyDropDemo: 体验QGraphicsView的拖放功能
- 远程FPGA平台上的Quartus II17.1 LCD色块闪烁现象解析