May 10, 2008 / Vol. 6, No. 5 / CHINESE OPTICS LETTERS 373
Enhanced Kerr nonlinearity in a negative refractive
atomic medium
Hongjun Zhang (
ÜÜÜ
ùùù
)
1,2,3
, Yueping Niu (
ÜÜÜ
±±±
)
1
, Hui Sun (
)
1
, and Shangqing Gong (
÷÷÷
ÿÿÿ
)
1
1
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics,
Chinese Academy of Sciences, Shanghai 201800
2
School of Physics and Information Technology, Shaanxi Normal University, Xi’an 710062
3
Graduate University of Chinese Academy of Sciences, Beijing 100049
Received December 13, 2007
The Kerr nonlinearity of a left-handed material is analyzed in a four-level atomic system. It is shown that,
due to the effect of quantum interference, a large enhanced Kerr nonlinearity accompanied by vanishing
absorption can be realized via choosing appropriate parameters in this negative refraction atomic medium.
It not only shows the large nonlinearity but also acts as the phase and amplitude compensating effects.
OCIS codes: 190.0190, 270.0270.
Recently, an interesting research ab out left-handed ma-
terial (LHM)
[1]
has attracted cons iderable attention be-
cause of its surprising and counterintuitive electromag-
netic and optical properties, such as the reversals of
both Doppler shift and Cerenkov effect
[1]
, amplification
of evanescent waves
[2]
, subwavelength focusing
[2,3]
, ab-
normal longitudinal and lateral shifts
[4,5]
. This mate-
rial has a negative refractive index when the permit-
tivity and permeability are negative simultaneously
[1]
.
In LHM, the wave vector is opposite to the direction
of energy propagation, so that this material acts as a
phase compensating effect in contrast to the ordinary
materials
[6]
. This makes it have the potential applica-
tions in perfectlens
[7,8]
and spatial filtering
[9]
. Up to
now, there are several approaches to the realization of
LHM, including artificial composite metamaterials
[10,11]
,
photonic cry stal structures
[12,13]
, and transmission line
simulation
[14]
as well as photonic resonant materia ls (co-
herent atomic vapor)
[15−19]
. Very recently, s ome non-
linear properties of LHM have been studied in meta-
materials, such as the hysteresis-type dependence of the
magnetic permeability on the field intensity
[20]
, second-
harmonic generation (SHG)
[21]
, optical parametric am-
plification (OPA)
[22]
, and optical bistability (OB)
[23]
. It
opens a new branch of nonlinear optics.
Although some linea r prop erties of LHM have bee n
studied in atomic sy stems
[15−19]
, to our knowledge, there
are few literatures to investigate the nonlinearity of a
negative refractive atomic medium. In this Letter, we
investigate the Kerr nonlinearity of LHM in a four-level
atomic system, where the neg ative refraction can be real-
ized by quantum coherence
[18]
. We find that the nonlin-
ear susceptibilities can be controlled by the control and
pump fields, and the focusing or defocusing effects oc-
cur in this left-handed material. We also find that a
large enhanced Kerr nonlinearity accompanied by van-
ishing absorption can be realized via choosing appropri-
ate parameters. Therefore, we may not only obtain the
large nonlinearity but also realize the phase compensat-
ing effect to the transmission wave and amplitude com-
pens ating effect to the evanescent wave.
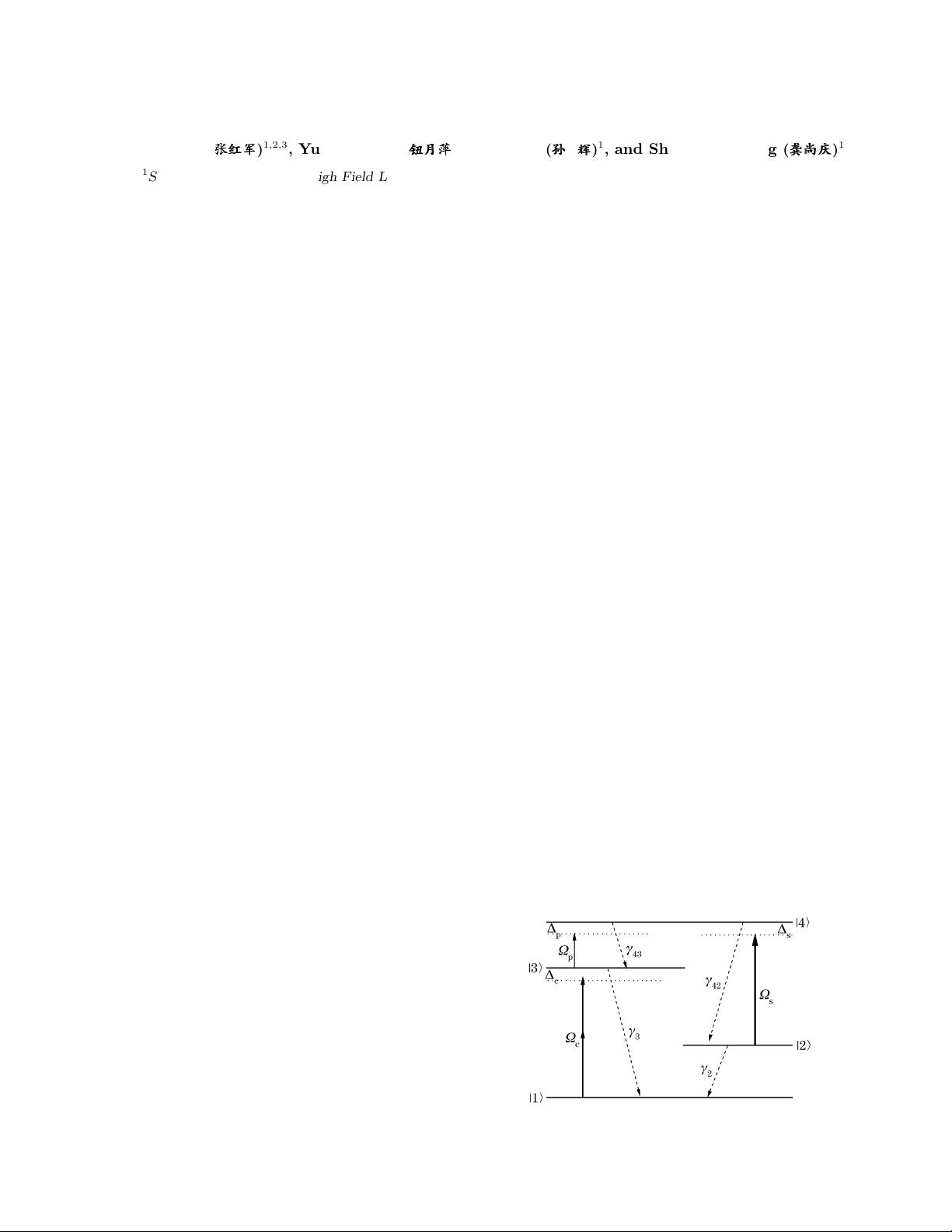
We consider a four-level atomic system as that in
Ref. [18], which is shown in Fig. 1. The two lower lev-
els |1i and |2i, have the same parity with the ma gnetic
dipole element µ
12
= h1|
ˆ
~µ |2i 6= 0. The two upper lev-
els |3i and |4i, which have opposite parity with electric
dipole element d
34
= h3|
ˆ
~
d |4i 6= 0, are coupled by a weak
probe electric field Ω
p
. The levels |1i and |3i are coupled
by a control field Ω
c
and levels |2i and |4i are c oupled
by a strong pump field Ω
s
. Here, Ω
i
(i = p, c, s) are the
Rabi frequencies of the probe, control, and pump fields
respectively and the transition |3i ↔ |1i is assumed to
be a two -photon process.
The Hamiltonian of the system with rotating-wave ap-
proximations reads
H = ¯h
0 0 −Ω
c
0
0 δ
12
0 −Ω
s
−Ω
c
0 δ
13
−Ω
p
0 −Ω
s
−Ω
p
δ
14
, (1)
where δ
12
= ∆
p
+ ∆
c
− ∆
s
, δ
13
= ∆
c
and δ
14
= ∆
p
+ ∆
c
,
in which ∆
p
= ν
p
− (ω
4
− ω
3
), ∆
c
= 2ν
c
− (ω
3
− ω
1
),
and ∆
s
= ν
s
− (ω
4
− ω
2
) denote the detunings of the
probe, control, and pump fields, respectively, and they
satisfy the relation ∆
c
= ∆
s
; ω
ij
= ω
i
− ω
j
is the tran-
sition frequency from levels |ii to |ji (i, j = 1, 2, 3, 4);
ν
i
(i = p, c, s) are the frequencies of the probe , c ontrol,
Fig. 1. Scheme of a four-level atom interacting with the probe,
pump, and control fields.
1671-7694/2008/050373-04
c
2008 Chinese O ptics Letters









