Received November 20, 2017, accepted January 27, 2018, date of publication February 27, 2018, date of current version March 15, 2018.
Digital Object Identifier 10.1109/ACCESS.2018.2809451
Distributed Kalman Filtering With Finite-Time
Max-Consensus Protocol
PENG LIU , YU-PING TIAN, AND YA ZHANG
School of Automation, Southeast University, Nanjing 210096, China
Key laboratory of Measurement and Control, Department of Computer Science and Engineering, Ministry of Education, Southeast University,
Nanjing 210096, China
Corresponding author: Yu-Ping Tian (yptian@seu.edu.cn)
This work was supported in part by the National Natural Science Foundation of China under Grant 61573105 and Grant 61473081,
and in part by the Natural Science Foundation of Jiangsu Province under Grant BK20141341.
ABSTRACT This paper investigates the distributed state estimation problem for an unstable dynamic plant
in a sparsely strongly connected sensors network. The dynamics of the plant are collectively observable for
all sensors, but not necessarily locally observable for each sensor. We propose a finite-time consensus-based
distributed estimator to cope with the local unobservability. This algorithm is based on the max-consensus
technique, and the number of consensus iterations is precisely provided. We prove that this estimator is stable
and the mean-squared error is equal to that obtained by the centralized estimator. Furthermore, we extend this
finite-time consensus Kalman filtering algorithm to networks with nonuniform time-varying communication
delays. By introducing the virtual nodes, which act as the relay nodes, we prove the stability of the algorithm.
Finally, the effectiveness of the proposed distributed finite-time consensus filters is evaluated by simulation
experiments.
INDEX TERMS Distributed Kalman filter, communication delays, finite-time consensus, max-consensus.
I. INTRODUCTION
For the past decades, sensor networks have received
significant attention of many researchers. The networks
are composed of tiny, power-constrained nodes with sens-
ing, computation, and wireless communication capabilities.
These nodes are usually distributed spatially to process a
limited amount of data, such as monitoring of environmental
attributes [1], [2], estimating the state of power networks [3],
tracking the moving objects by the camera networks [4], [5]
and distinguishing the orbital debris using radars and optical
telescopes [6]. The features of energy and channel capac-
ity constraints render the centralized estimator impractical,
which motivates researchers to focus on the distributed esti-
mation protocols. The advantages of the distributed proto-
cols include the scalability for large-scale networks and high
fault tolerance. For distributed estimation problem, multiple
sensors can sense the target (or plant), each sensor may get
partial or no measurements related to the state of a target.
The aim of a distributed estimator is to reconstruct an esti-
mate of the target’s state using its local measurement and
its neighbor’s information in the network without requiring
a centralized node for information fusion. An agreement
on the gathered information can be reached via consensus
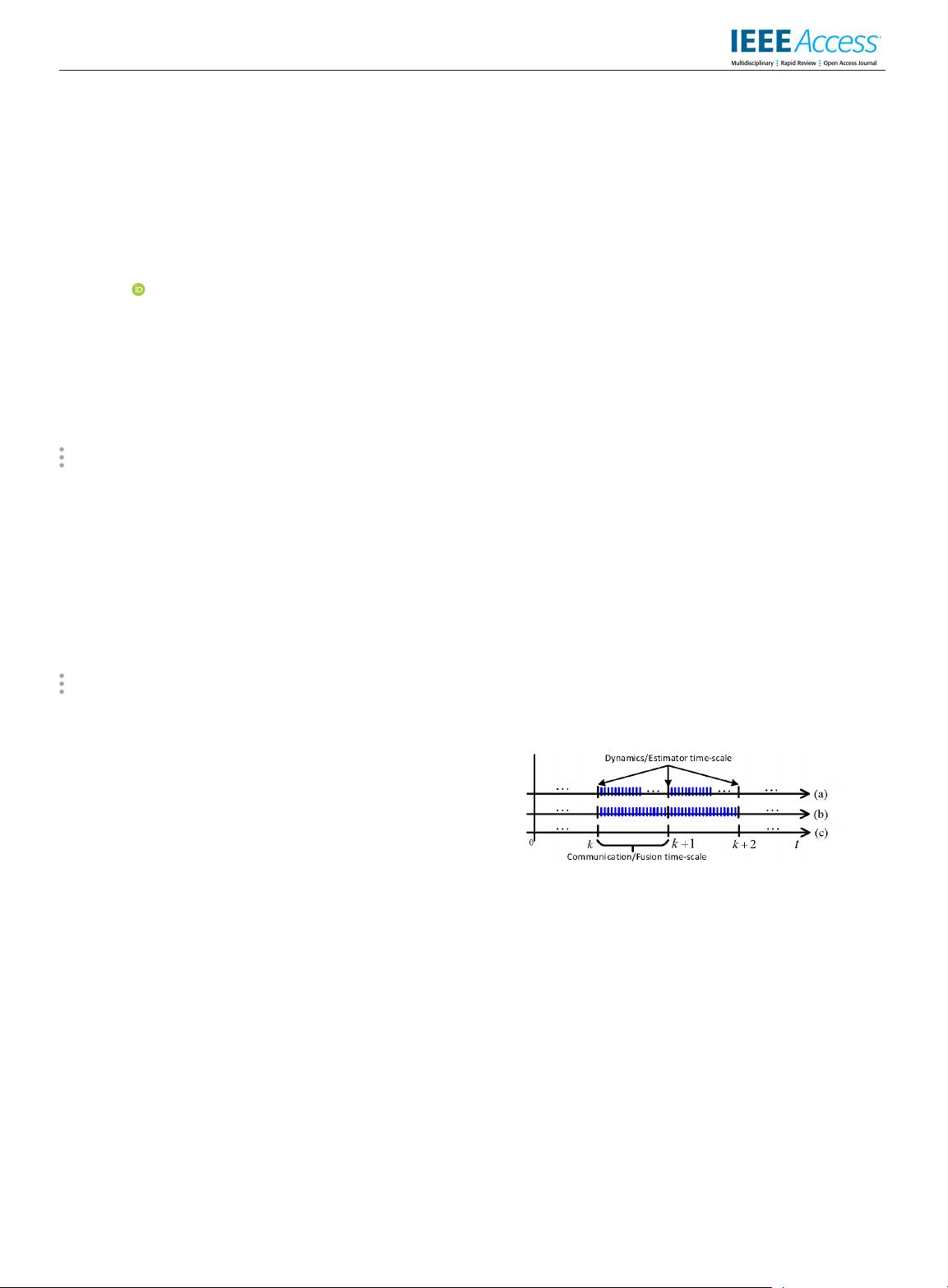
FIGURE 1. Three different time-scales.
algorithms. Consensus protocols are extensively studied
in formation of multi-agent, distributed estimation, and
distributed optimization problems, etc. Generally speaking,
consensus problem is different from the term distributed
estimation, which refers to using the consensus algorithms
for finding the best estimate of the target. This paper studies
the distributed filtering algorithms with finite-time consensus
strategy.
Distributed estimators (such as distributed Kalman filter
and its transformed forms) for dynamic systems have gained
considerable attention [7]–[10]. The existing research on
distributed estimation can be classified into two categories
based on the principle of operation: 1) two time-scale: fast
communication-slow dynamics and sensing, see Fig.1.(a) and
VOLUME 6, 2018
2169-3536 2018 IEEE. Translations and content mining are permitted for academic research only.
Personal use is also permitted, but republication/redistribution requires IEEE permission.
See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
10795









