Any Curve Path Following of Snake-like Robots
Xian Guo, Wei Zhu, and Yongchun Fang
Institute of Robotics and Automatic Information Systems
University of Nankai
Tianjin,300350 China
fangyc@nankai.edu.cn
Abstract— Because of redundant freedoms, designing a robust
any path following controller for snake-like robots is very
challenging. In this paper, a novel path following controller,
combining the robust following controller used in the unicycle
robot and the fiber bundle model of snake-like robots, is
proposed to follow any planar curve. More specifically, firstly,
the kinematic model is established based on the fiber bundle
theory which connects snake-like robots and unicycle robots.
Then the robust path following controller for the unicycle
robots is modified to be applied to the sake-like robots. Finally,
to obtain a feasible controller, an estimation method for the
orientation angle of the robot in the fiber bundle is proposed.
To validate the proposed method, numerical simulations and
experiments are performed. The results demonstrate that the
proposed following controller is robust and valid.
Index Terms— Snake-like robots, Path following, Geometric
mechanics, Any planar curve.
I. INTRODUCTION
Since 1970s, the research about snake-like robots has
attracted wide and lasting attentions of scholars from all
over the world, because the snake-like robots can move in
various environments such as land, ocean, forest, desert, etc.
The main topics are focused on methods how to generate
various gaits to adapt to different environments. Among
these methods, three methods are commonly used: curve-
based method [1], CPG-based method [2], and model-based
method [3] [4]. These works are very useful and have
brought about many achievements, such as swimming, climb-
ing pipelines, searching and rescuing in disastrous sites.
However, the control used in most of these work is either
semi-automatic or completely manual, meaning the robots
lack in autonomy. Generally speaking, path planning and
path following methods are needed for a fully autonomous
robot. Firstly, a desired path connecting the start point and
the end point is derived by path planning methods such as
graph search based methods [5] [6], sampling-based methods
[7] [8], interpolating curve based methods[9] or numerical-
optimization-based methods [10]. Then, a closed-loop path
following controller is designed to enable the robot to track
∗
This work is supported by National Natural Science Foundation
of China(GrantNo.61603200,GrantNo.U1613210) X. Guo, W. Zhu and
Y. Fang are with the Institute of Robotics and Automatic Informa-
tion Systems, Nankai University, Tianjin 300350, China (e-mail: guox-
ian@nankai.edu.cn;zhuwei@mail.nankai.edu.cn; fangyc@nankai.edu.cn)
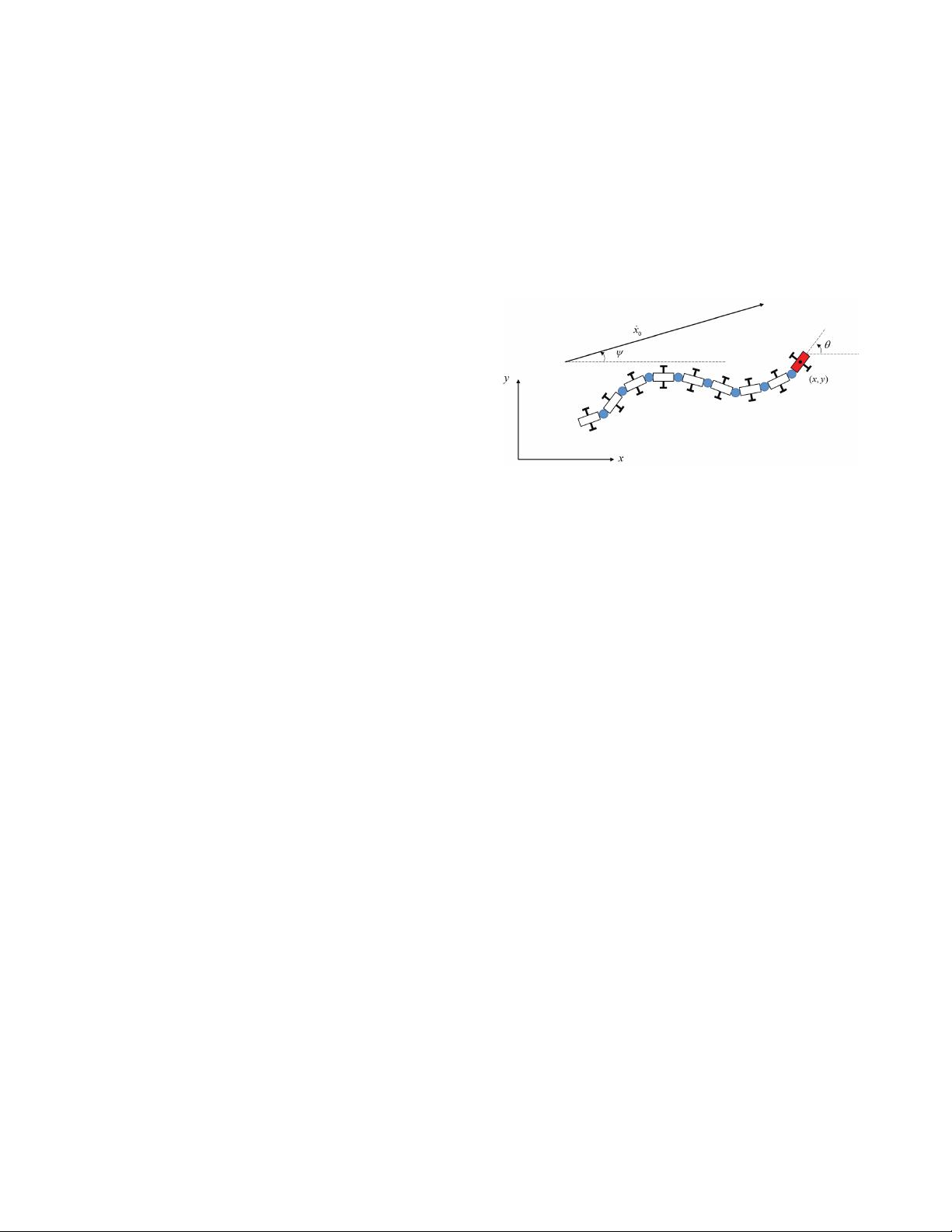
Fig. 1. Snake-like robots with passive wheels. The coordinates of the head
is (x, y, θ). ˙x
0
denotes the velocity of the snake robots, and ψ denotes the
turning angle of the whole snake-like robot.
the desired path. Additionally, the path following method is
also needed when a specified curve is given to finish some
special task. In this paper, the topic about path following for
snake-like robots is discussed.
In fact, path following methods have been deeply re-
searched for the unicycle vehicle. The most popular one is
the projection method such as LOS (Line-of-Sight) Guid-
ance method[11] and Integral Line-of-Sight Guidance method
[12], in which the projection point on the desired path
is firstly computed together with the distance and angular
errors being recalculated, then various nonlinear controller
is designed based on Lyapunov function or sliding mode
techniques [13]. For a simple curve following, they work
very well. However, there is one critical drawback to these
methods: the projection point must be unique which requires
the initial point can not be too far from the desired curve and
the desired curve can not be too complex. In order to solve
the non-uniqueness of the projection method, a virtual target
method is proposed, in which an explicit progression rate of
the moving target method is tracked [14]. Unfortunately, the
asymptotic convergence to the path can not be guaranteed.
Morro proposes a new feedback control model which can
guarantee asymptotic convergence to any 2-D curve neither
requiring the projection nor considering a moving virtual
target[15]. However, the controller is only applicable to
unicycle robots.









