COL 10(1), 013104(2012) CHINESE OPTICS LETTERS January 10, 2012
Dependence of wavefront errors on
nonuniformity of thin films
Hongji Qi (齐齐齐红红红基基基)
∗
, Meiping Zhu (朱朱朱美美美萍萍萍), Weili Zhang (张张张伟伟伟丽丽丽),
Kui Yi (易易易 葵葵葵), Hongbo He (贺贺贺洪洪洪波波波), and Jianda Shao (邵邵邵建建建达达达)
Key Laboratory of Material Science and Technology for High Power Lasers,
Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201800, China
∗
Corresp onding author: qhj@siom.ac.cn
Received April 2, 2011; accepted May 13, 2011; posted online July 29, 2011
In contrast to uncoated substrate, a nonlinear relationship of phase shift with the thicknesses of the thin
film makes the calculation of wavefront aberration complicated. A program is compiled to calculate the
wavefront aberration of multilayer thin film produced by thickness nonuniformity. The physical thickness
and the optical phase change on reflection are considered. As an example, the wavefront aberration of the
all-dielectric mirror is presented in ArF excimer lithography system with a typical thickness distribution.
In addition, the wavefront errors of the thin film at wavelengths of 193 and 633 nm are compared in the
one-piece and two-piece arrangements. Results show that the phase shift upon reflection of the thin film
pro duced by thickness nonuniformity is very sensitive to the incident angle, wavelength, and polarization.
OCIS codes: 310.6870, 000.4430, 050.5080.
doi: 10.3788/COL201210.013104.
In order to prevent the distortion of the beam profile,
the perfect flatness specification of surface should be
achieved for all the optical components. In a stadium-
sized laser facility – National Ignition Facility (NIF) at
the Lawrence Livermore National Laboratory – meter-
scale laser coatings, e.g., reflector, must meet the wave-
front requirement of λ/3 (λ = 1 053 nm)
[1]
. Because the
phase change is proportional to 1/λ, wavefront control is
more difficult for optical components in the ultra-violet
(UV) laser system compared with those in the infrared
system. In the UV lithographic system, the surface flat-
ness of optical components should be strictly controlled
to enhance the exposure resolution in the illumination,
imaging, and exposure systems. Compared with the
uncoated substrate, the flatness of the coated optical
components is determined by more factors
[2−6]
. In ad-
dition, the dependence of wavefront error on nonuni-
formity must be considered for the meter-scale-size
optical components. Ramsay et al. investigated the
multilayer dielectric reflecting surfaces in Fabry-Perot
interferometers
[7]
. Knowlden calculated the wavefront
errors produced by nonuniformity for dielectric-enhanced
infrared reflectors
[8]
.
In this letter, on the basis of the “figure error” func-
tion module in the Essential Macloed software, a program
was compiled to calculate the wavefront aberration due
to nonuniformity. The physical thickness and the optical
phase change on reflection due to thickness nonuniformity
were considered. The calculated results were input into
the MetroPro software to construct three-dimentional
(3D) surface morphology. As an example, the wavefront
aberration of the all-dielectric mirror was presented in
ArF lithography system. In addition, the wavefront of
the thin film at wavelengths of 193 and 633 nm were
compared with nonuniformity of 2%.
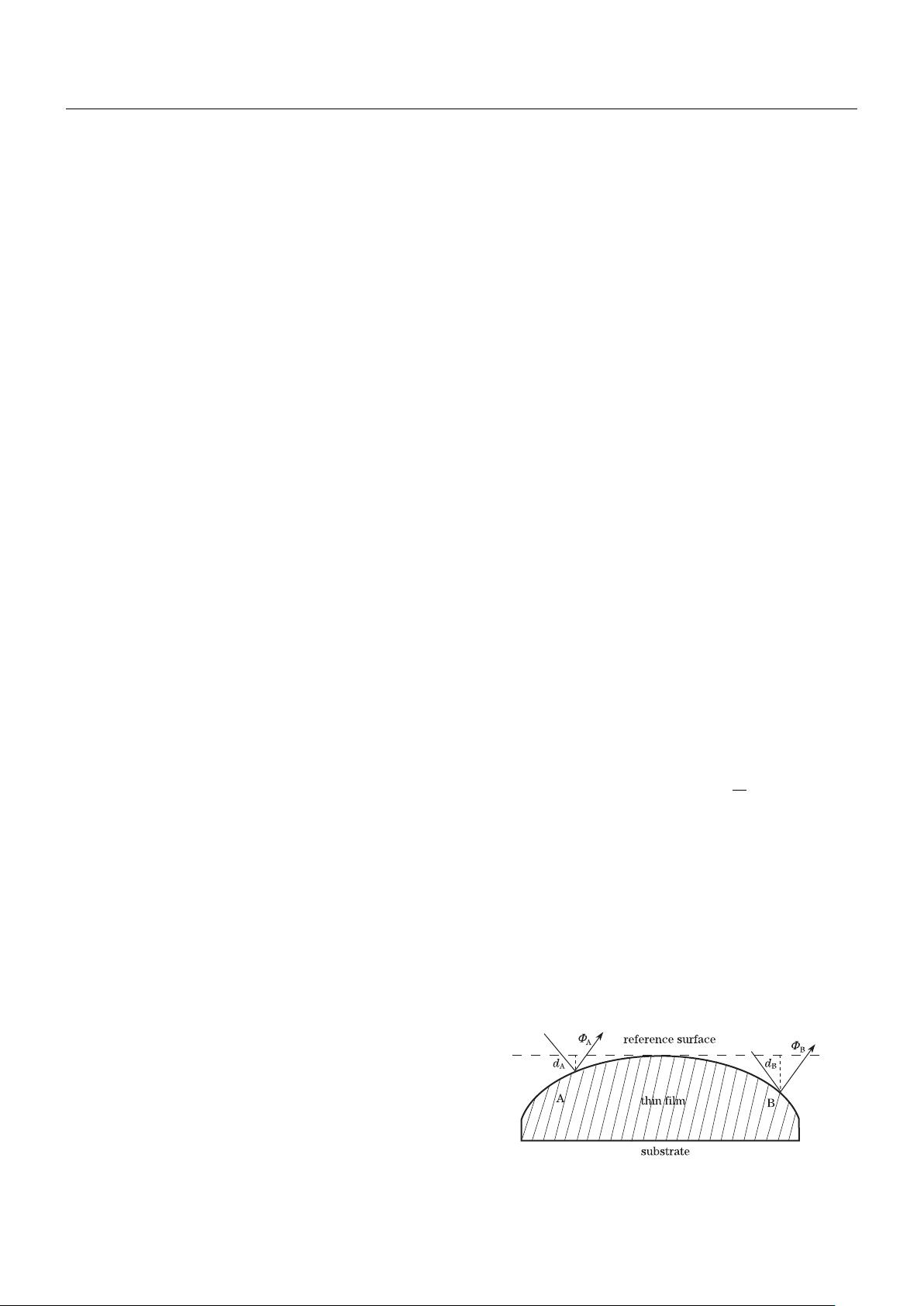
For an uncoated optical surface, wavefront distortion
is only related to figure error, i.e., the physical thickness
modulation of the surface. In the reflection approach,
the wavefront error is simply twice that of the surface.
In the case of coated optical surface, the phase shift
upon reflection of the multilayer thin film is involved in
the measurement of wavefront distortion, as shown in
Fig. 1. The total phase shift difference, Φ
A
–Φ
B
, de-
pends on the physical thickness difference, d
A
–d
B
, and
the reflective phase shift difference, Φ(d
A
)–Φ(d
B
). The
phase shift difference ∆Φ related to the physical thick-
ness difference, ∆d = d
A
–d
B
, is given by the formula ∆Φ
= ∆d/λ. The relationship between the reflective phase
shift difference Φ(d
A
)–Φ(d
B
) and the physical thickness
difference ∆d is relatively complicated.
In the case of isotropic film, the jth layer
film can be described by the characteristic matrix
h
cos δ
j
i sin δ
j
/η
j
iη
j
sin δ
j
cos δ
j
i
, where δ
j
=
2π
λ
n
j
d
j
cos θ
j
is re-
ferred as the phase thickness; n
j
and d
j
are the refractive
index and the physical thickness of the film, respectively;
η
j
is the effective optical admittance; θ
j
is the refractive
angle in the jth layer film. Combined with the substrate
or emergent medium with effective optical admittance
η
m
, the characteristic matrix of an assembly of q layers is
shown as
h
B
C
i
=
q
Q
j=1
h
cos δ
j
i sin δ
j
/η
j
iη
j
sin δ
j
cos δ
j
i
·
h
1
η
m
i
.
Here, B and C are the normalized electric and magnetic
fields at the front interface and can be used to extract
the properties of the thin film system, including the
phase change upon reflection, as shown by the equation
Fig. 1. Physical thickness and phase shift upon reflection pro-
duced by nonuniform coating.
1671-7694/2012/013104(4) 013104-1
c
° 2012 Chinese Optics Letters









