Treap深度解析：理论与实战应用

"Treap分析与应用" Treap是一种结合了随机性的平衡二叉查找树（BST），由Seidel在1989年提出，它在信息学竞赛和算法设计中有着广泛的应用。这种数据结构巧妙地将二叉查找树的特性与堆的随机化属性结合在一起，从而保证了较好的平衡性能，提高了查找、插入和删除操作的效率。 在二叉查找树中，每个节点包含一个键值和两个子节点，左子节点的键值小于当前节点，右子节点的键值大于当前节点。然而，这种结构在最坏情况下可能导致树的高度线性，即退化成链表，这会严重影响查找效率。为了解决这个问题，平衡二叉查找树如AVL树和红黑树应运而生，它们通过特定的规则保持树的平衡，确保查找、插入和删除的时间复杂度为O(log n)。 Treap的创新之处在于引入了随机化元素。每个节点不仅有键值，还有一个优先级，优先级是随机生成的，通常用一个伪随机数生成器来设定。在构建和操作Treap时，除了根据键值进行比较外，还会依据优先级进行调整，以保持树的平衡。因此，即使在最坏的情况下，Treap的期望高度依然保持为O(log n)，在实际应用中表现出良好的性能。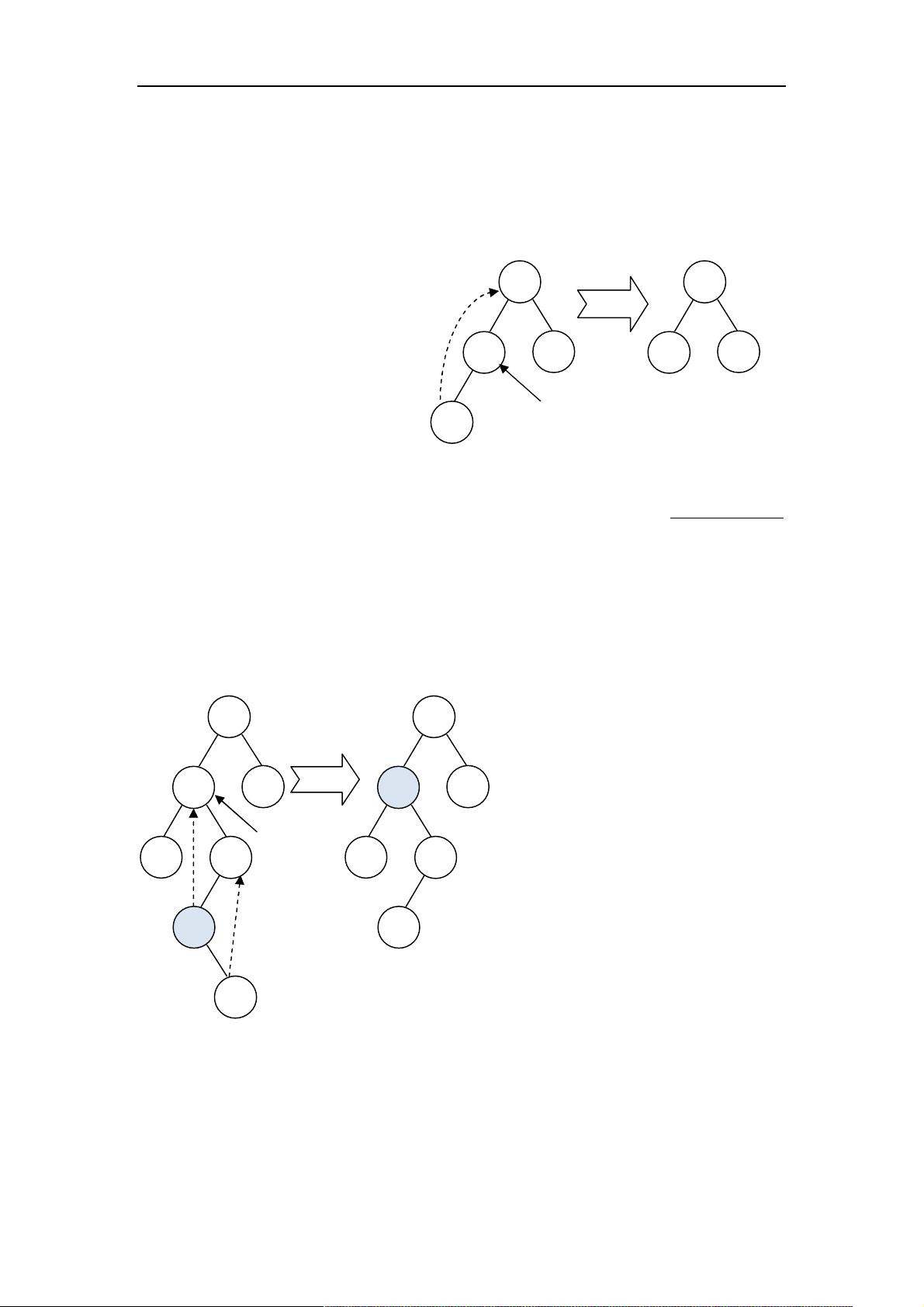 Treap的构造方法包括插入和删除操作。插入新节点时，首先按照键值将其放在正确的位置，然后根据优先级调整树的结构。删除节点时，需要找到要删除的节点，更新其父节点和子节点，同时保持堆的性质。由于随机优先级的存在，这些操作通常比在其他平衡树中更简单。 Treap在算法设计中的应用非常多样化。在动态统计问题中，Treap可以快速地进行区间查询和更新，例如计算区间内元素的和或者找到区间内的最大值。在搜索问题中，Treap可以帮助高效地查找满足特定条件的元素。在动态规划问题中，Treap可以用于维护部分状态，动态更新解空间，从而减少计算量。 此外，Treap还可以与其他数据结构结合，如用于构建动态字典树、解决区间最值问题等。其简洁的实现和灵活的特性使得Treap成为解决复杂问题的一个有力工具。 总结来说，Treap是一种具有随机平衡特性的数据结构，它通过随机优先级保证了树的平衡性，提供了高效的查找、插入和删除操作，尤其适用于动态变化的数据集和信息学竞赛中的算法设计。尽管它可能不如某些经典平衡树结构那样严格平衡，但在实际应用中，它的平均性能往往足以满足需求，且代码实现相对简洁，易于理解。