神经网络的通用性：计算任何连续函数的视觉证明

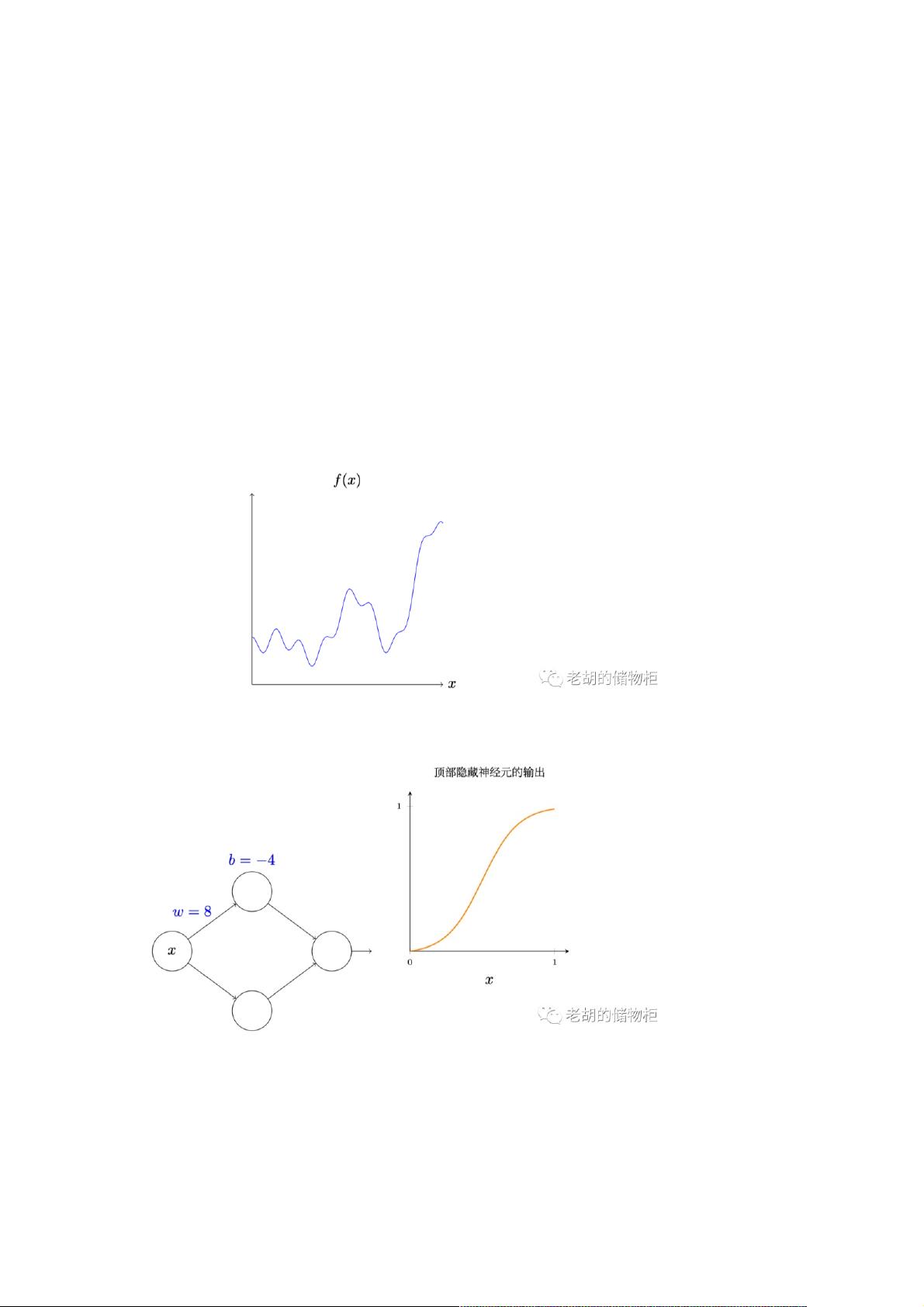
本篇文章主要来源于《Neural Networks and Deep Learning》第四篇读书笔记，探讨了神经网络的一种关键特性——普遍性。神经网络被证明具有强大的计算能力，无论目标函数多么复杂，都可以近似任何可能的输入，输出其值或者近似值。这一特性使得我们相信存在一个多层神经网络能够解决各种复杂的函数计算问题，例如自然语言处理（如中文到英文的翻译）、视频分析（如根据MP4生成电影描述）等。 作者强调了神经网络的局限性，虽然理论上可以计算任何连续函数，但实际应用中可能存在精度和性能的限制。网络的性能取决于隐藏单元的数量，通过增加隐藏单元可以提高近似精度，但必须设定一个合理的精度范围。值得注意的是，神经网络的计算能力主要针对的是连续函数，对于非连续的函数，特别是那些具有突然跳跃的函数，神经网络可能无法提供完美的近似。 文章还提到了两个预先声明：神经网络并不能精确地计算所有函数，而是提供近似解；而且，含有多个隐藏层的神经网络能够实现更高精度的逼近。接着，作者用一个简单的单输入单输出的函数为例，展示了如何通过一个带有隐藏层的神经网络进行近似，这里提及了一种S型神经元，其输出范围类似于特定函数的图形。 接下来的部分会进一步阐述如何通过一个仅含一个隐藏层的神经网络来证明普遍性定理的弱化版本，并可能涉及具体的构造和证明过程。这篇文章深入浅出地揭示了神经网络的普遍性在理论与实践中的应用价值，以及在面对复杂函数时的局限性和优化策略。