深度学习驱动的人脸识别最新进展综述

3星 · 超过75%的资源需积分: 44 120 浏览量更新于2024-07-17 3 收藏 5.85MB PDF 举报

人脸识别作为生物识别技术中的一个重要分支，近年来受益于深度学习的快速发展，其性能得到了显著提升并广泛应用于实际场景。本篇综述论文《DeepFaceRecognition: A Survey》由Mei Wang和Weihong Deng两位作者撰写，他们分别来自北京邮电大学信息与通信工程学院。论文旨在提供对深度学习在人脸识别（deep face recognition, deepFR）领域最新进展的全面概述。论文首先阐述了深度学习如何通过多层处理网络来提取数据的多层次特征，这种新兴技术自2014年深度面部识别方法取得突破以来，就重塑了人脸识别研究的格局。深度FR技术利用层次结构将像素融合成不变的脸部表示，极大地提高了识别准确率，并推动了实际应用的成功。作者在文中详细梳理了深度FR方法的快速演进历程。他们总结了各种网络架构的设计，这些架构包括但不限于卷积神经网络（Convolutional Neural Networks, CNN）、残差网络（Residual Networks, ResNets）、注意力机制（Attention Mechanisms）等，这些都在人脸特征提取和识别过程中发挥了关键作用。此外，论文还探讨了不同的损失函数，如softmax、中心损失（Center Loss）、对比性损失（Contrastive Loss）等，它们对于模型的学习和优化至关重要。在脸部处理方法方面，文章将相关技术分为两大类：一是特征提取，如特征金字塔网络（Feature Pyramid Networks, FPN）、局部二值模式（Local Binary Patterns, LBP）等；二是人脸对齐与归一化，如Morphable Models、3D人脸重建等，这些技术确保了不同姿态和光照条件下的人脸都能被准确地识别。论文接着讨论了数据库的发展，涵盖了公开的人脸识别基准数据集，如LFW、CelebA、VGGFace、MS-Celeb-1M等，以及随着大数据和云计算带来的新挑战和机遇。同时，作者分析了人脸识别协议和标准，如FaceNet的嵌入式特征、OpenFace的实时性优化，以及FR在安全验证、身份验证、监控系统和虚拟现实等多个应用场景中的应用实例。这篇综述论文不仅深入剖析了深度学习在人脸识别领域的技术进步，还为研究人员和开发者提供了关于算法设计、数据管理和实际应用的实用指南，有助于推动该领域进一步发展和创新。

tions inherit from object classiﬁcation and develop according

to unique characteristics of FR; face processing methods are

also designed to handle poses, expressions and occlusions

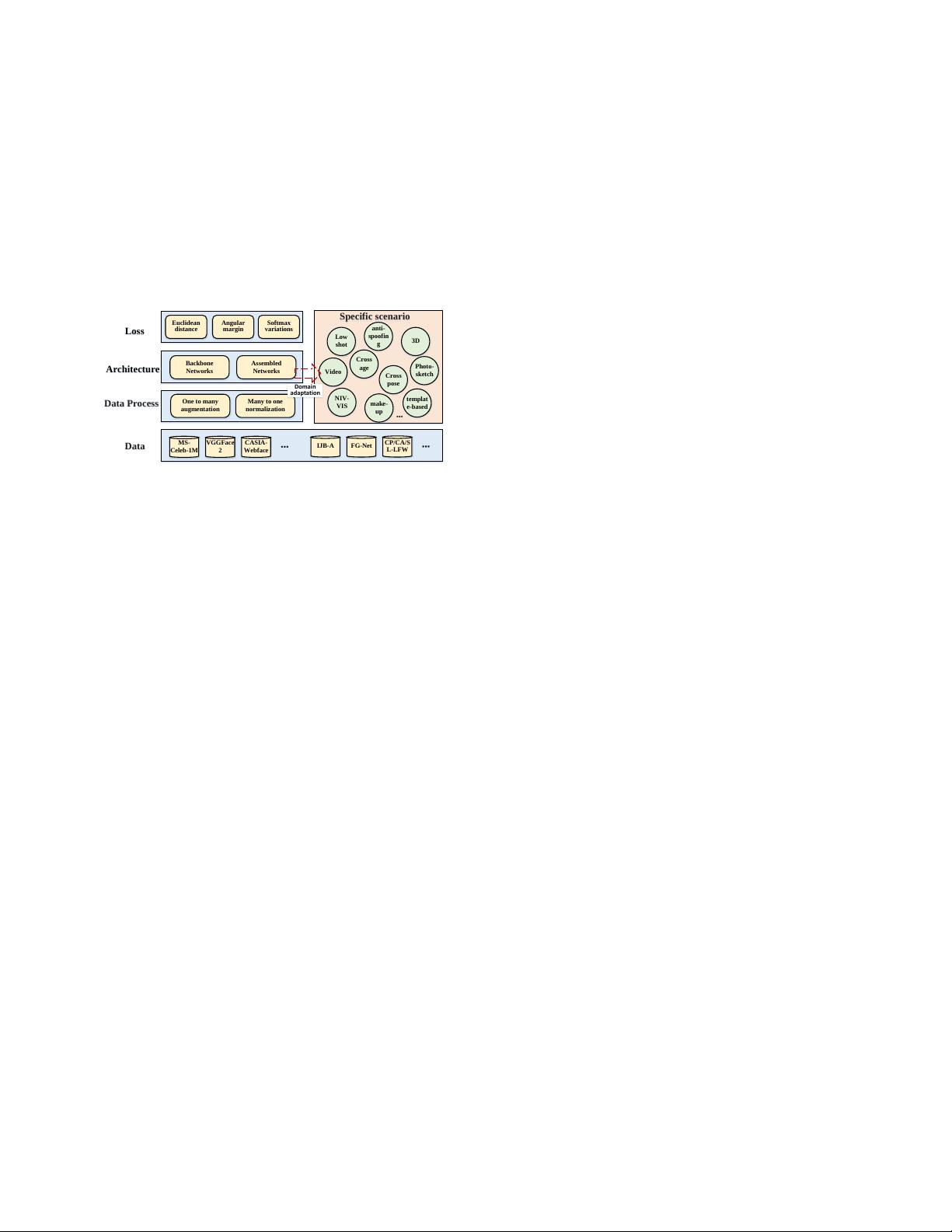
variations. With maturity of FR in general scenario, difﬁculty

levels are gradually increased and different solutions are driven

for speciﬁc scenarios that are closer to reality, such as cross-

pose FR, cross-age FR, video FR. In speciﬁc scenarios, more

difﬁcult and realistic datasets are constructed to simulate

reality scenes; face processing methods, network architectures

and loss functions are also modiﬁed based on those of general

solutions.

Data

Data Process

Architecture

Loss

Euclidean

distance

Angular

margin

Softmax

variations

Backbone

Networks

Assembled

Networks

One to many

augmentation

Many to one

normalization

Video

Low

shot

Photo-

sketch

…

anti-

spoofin

make-

Domain

adaptation

MS-

Celeb-1M

VGGFace

CASIA-

Webface

…

IJB-A FG-Net

CP/CA/S

L-LFW

…

NIV-

VIS

templat

e-based

Cross

age

Cross

pose

Specific scenario

Fig. 4. FR studies have begun with general scenario, then gradually increase

difﬁculty levels and drive different solutions for speciﬁc scenarios to get close

to reality, such as cross-pose FR, cross-age FR, video FR. In speciﬁc scenarios,

targeted training and testing database are constructed, and the algorithms, e.g.

face processing, architectures and loss functions are modiﬁed based on those

of general solutions.

III. NETWORK ARCHITECTURE AND TRAINING LOSS

As there are billions of human faces in the earth, real-

world FR can be regarded as an extremely ﬁne-grained object

classiﬁcation task. For most applications, it is difﬁcult to

include the candidate faces during the training stage, which

makes FR become a “zero-shot” learning task. Fortunately,

since all human faces share a similar shape and texture, the

representation learned from a small proportion of faces can

generalize well to the rest. A straightforward way is to include

as many IDs as possible in the training set. For example,

Internet giants such as Facebook and Google have reported

their deep FR system trained by 10

− 10

IDs [176], [195].

Unfortunately, these personal datasets, as well as prerequisite

GPU clusters for distributed model training, are not accessible

for academic community. Currently, public available training

databases for academic research consist of only 10

−10

IDs.

Instead, academic community make effort to design effec-

tive loss functions and adopt deeper architectures to make deep

features more discriminative using the relatively small training

data sets. For instance, the accuracy of most popular LFW

benchmark has been boosted from 97% to above 99.8% in the

pasting four years, as enumerated in Table IV. In this section,

we survey the research efforts on different loss functions and

network architecture that have signiﬁcantly improved deep FR

methods.

A. Evolution of Discriminative Loss Functions

Inheriting from the object classiﬁcation network such as

AlexNet, the initial Deepface [195] and DeepID [191] adopted

cross-entropy based softmax loss for feature learning. After

that, people realized that the softmax loss is not sufﬁcient by

itself to learn feature with large margin, and more researchers

began to explore discriminative loss functions for enhanced

generalization ability. This become the hottest research topic

for deep FR research, as illustrated in Fig. 5. Before 2017,

Euclidean-distance-based loss played an important role; In

2017, angular/cosine-margin-based loss as well as feature and

weight normalization became popular. It should be noted that,

although some loss functions share similar basic idea, the new

one is usually designed to facilitate the training procedure by

easier parameter or sample selection.

1) Euclidean-distance-based Loss : Euclidean-distance-

based loss is a metric learning method[230], [216] that embeds

images into Euclidean space and compresses intra-variance

and enlarges inter-variance. The contrastive loss and the triplet

loss are the commonly used loss functions. The contrastive loss

[222], [187], [188], [192], [243] requires face image pairs and

then pulls together positive pairs and pushes apart negative

pairs.

L =y

max



0, kf(x

) − f (x

− 



+ (1 − y

)max



0, 

−

− kf(x

) − f (x



(2)

where y

= 1 means x

and x

are matching samples and

= −1 means non-matching samples. f (·) is the feature

embedding, 

and 

−

control the margins of the matching and

non-matching pairs respectively. DeepID2 [222] combined the

face identiﬁcation (softmax) and veriﬁcation (contrastive loss)

supervisory signals to learn a discriminative representation,

and joint Bayesian (JB) was applied to obtain a robust embed-

ding space. Extending from DeepID2 [222], DeepID2+ [187]

increased the dimension of hidden representations and added

supervision to early convolutional layers, while DeepID3 [188]

further introduced VGGNet and GoogleNet to their work.

However, the main problem with the contrastive loss is that

the margin parameters are often difﬁcult to choose.

Contrary to contrastive loss that considers the absolute

distances of the matching pairs and non-matching pairs, triplet

loss considers the relative difference of the distances between

them. Along with FaceNet [176] proposing by Google, Triplet

loss [176], [149], [171], [172], [124], [51] was introduced

into FR. It requires the face triplets, and then it minimizes

the distance between an anchor and a positive sample of the

same identity and maximizes the distance between the anchor

and a negative sample of a different identity. FaceNet made

kf(x

) − f (x

+ α < − kf (x

) − f (x

using hard

triplet face samples, where x

, x

and x

are the anchor,

positive and negative samples, respectively; α is a margin;

and f (·) represents a nonlinear transformation embedding

an image into a feature space. Inspired by FaceNet [176],

TPE [171] and TSE [172] learned a linear projection W to

construct triplet loss, where the former satisﬁed Eq. 3 and the

latter followed Eq. 4. Other methods combine triplet loss with

softmax loss [276], [124], [51], [40]. They ﬁrst train networks

with the softmax and then ﬁne-tune them with triplet loss.

)

W x

+ α < (x

)

W x

(3)

TABLE IV

THE ACCURACY OF DIFFERENT VERIFICATION METHODS ON THE LFW DATASET.

Method

Public.

Time

Loss Architecture

Number of

Networks

Training Set Accuracy±Std(%)

DeepFace [195] 2014 softmax Alexnet 3 Facebook (4.4M,4K) 97.35±0.25

DeepID2 [187] 2014 contrastive loss Alexnet 25 CelebFaces+ (0.2M,10K) 99.15±0.13

DeepID3 [188] 2015 contrastive loss VGGNet-10 50 CelebFaces+ (0.2M,10K) 99.53±0.10

FaceNet [176] 2015 triplet loss GoogleNet-24 1 Google (500M,10M) 99.63±0.09

Baidu [124] 2015 triplet loss CNN-9 10 Baidu (1.2M,18K) 99.77

VGGface [149] 2015 triplet loss VGGNet-16 1 VGGface (2.6M,2.6K) 98.95

light-CNN [225] 2015 softmax light CNN 1 MS-Celeb-1M (8.4M,100K) 98.8

Center Loss [218] 2016 center loss Lenet+-7 1

CASIA-WebFace, CACD2000,

Celebrity+ (0.7M,17K)

99.28

L-softmax [126] 2016 L-softmax VGGNet-18 1 CASIA-WebFace (0.49M,10K) 98.71

Range Loss [261] 2016 range loss VGGNet-16 1

MS-Celeb-1M, CASIA-WebFace

(5M,100K)

99.52

L2-softmax [157] 2017 L2-softmax ResNet-101 1 MS-Celeb-1M (3.7M,58K) 99.78

Normface [206] 2017 contrastive loss ResNet-28 1 CASIA-WebFace (0.49M,10K) 99.19

CoCo loss [130] 2017 CoCo loss - 1 MS-Celeb-1M (3M,80K) 99.86

vMF loss [75] 2017 vMF loss ResNet-27 1 MS-Celeb-1M (4.6M,60K) 99.58

Marginal Loss [43] 2017 marginal loss ResNet-27 1 MS-Celeb-1M (4M,80K) 99.48

SphereFace [125] 2017 A-softmax ResNet-64 1 CASIA-WebFace (0.49M,10K) 99.42

CCL [155] 2018 center invariant loss ResNet-27 1 CASIA-WebFace (0.49M,10K) 99.12

AMS loss [205] 2018 AMS loss ResNet-20 1 CASIA-WebFace (0.49M,10K) 99.12

Cosface [207] 2018 cosface ResNet-64 1 CASIA-WebFace (0.49M,10K) 99.33

Arcface [42] 2018 arcface ResNet-100 1 MS-Celeb-1M (3.8M,85K) 99.83

Ring loss [272] 2018 Ring loss ResNet-64 1 MS-Celeb-1M (3.5M,31K) 99.50

2014 2015 2016 2017

2018

Contrastive loss Triplet loss Center loss

Feature and weight normalization

Large margin loss

Softmax loss

Deepface

(softmax)

Center loss

(center loss)

FaceNet

(triplet loss)

Normface

(feature

normalization)

AMS loss

(large margin)

L-softmax

(large margin)

A-softmax

(large margin)

TPE

(triplet loss)

Arcface

(large margin)

VGGface

(triplet+softmax)

DeepID

(softmax)

DeepID2

(contrastive loss)

DeepID2+

(contrastive loss)

DeepID3

(contrastive loss)

TSE

(triplet loss)

Range loss

Marginal loss

L2 softmax

( feature

normalization)

vMF loss

(weight and feature

normalization)

Center

invariant loss

(center loss)

CoCo loss

(feature

normalization)

Cosface

(large margin)

Fig. 5. The development of loss functions. It marks the beginning of deep FR that Deepface [195] and DeepID [191] were introduced in 2014. After

that, Euclidean-distance-based loss always played the important role in loss function, such as contractive loss, triplet loss and center loss. In 2016 and 2017,

L-softmax [126] and A-softmax [125] further promoted the development of the large-margin feature learning. In 2017, feature and weight normalization also

begun to show excellent performance, which leads to the study on variations of softmax. Red, green, blue and yellow rectangles represent deep methods with

softmax, Euclidean-distance-based loss, angular/cosine-margin-based loss and variations of softmax, respectively.

−x

)

W (x

−x

)+α < (x

−x

)

W (x

−x

)

(4)

However, the contrastive loss and triplet loss occasionally

encounter training instability due to the selection of effective

training samples, some paper begun to explore simple alter-

natives. Center loss [218] and its variant [261], [43], [228]

is a good choice to compresses intra-variance. In [218], the

center loss learned a center for each class and penalized the

distances between the deep features and their corresponding

class centers. This loss can be deﬁned as follows:

i=1

− c

(5)

where x

denotes the ith deep feature belonging to the y

class and c

denotes the y

th class center of deep features.

To handle the long-tailed data, A range loss [261] is used

to minimize k greatest range’s harmonic mean values in one

class and maximize the shortest inter-class distance within one

batch, while Wu et al. [228] proposed a center-invariant loss

that penalizes the difference between each center of classes.

Deng et al. [43] selected the farthest intra-class samples and

the nearest inter-class samples to compute a margin loss.

However, the center loss and its variant suffer from massive

GPU memory consumption on the classiﬁcation layer, and

prefer balanced and sufﬁcient training data for each identity.

2) Angular/cosine-margin-based Loss : In 2017, people

had a deeper understanding of loss function in deep FR and

thought that samples should be separated more strictly to avoid

misclassifying the difﬁcult samples. Angular/cosine-margin-

based loss [126], [125], [205], [42], [127] is proposed to

剩余25页未读，继续阅读

一片绿色

粉丝: 0
资源: 1

深度学习驱动的人脸识别最新进展综述

人脸识别技术综述：从概念到应用

基于K-L变换PCA的特征脸人脸识别技术综述

异质人脸识别现状与挑战：综述与发展趋势

论文研究-三维人脸识别研究综述 .pdf

人脸识别综述(模式识别论文).doc

人脸识别综述与展望论文

人脸识别技术综述.PDF

人脸识别综述论文（几篇在维普上下的论文）

人脸识别研究综述参考.pdf

《端到端人脸识别》2020综述论文

最新资源